二次根式思维导图整理,轻松理清相关知识
2023-07-17 16:00:12
二次根式在数学中占据着重要的地位,它是数学中的一种基本代数表达式。为了更好地理解和应用二次根式,我们可以通过思维导图的方式整理相关知识。接下来,本文将从二次根式的概念、性质、运算等方面整理二次根式的思维导图,感兴趣的小伙伴们快看过来。
在思维导图中,我们可以将二次根式的概念作为中心节点,然后根据不同的性质,划分出各个分支。比如,可以有一个分支表示二次根式的简化方法,另一个分支表示二次根式的加减法则,还可以有一个分支表示二次根式的乘除法则等等。通过这样的思维导图,我们可以清晰地了解二次根式的各个方面,更好地应用于实际问题的解决过程中。
(2)性质:
①当a≥0时,√a≥0
②当a≥0时,(√a)²=a
③当a≥0时,√a²=|a|=a
④当a<0时,√a²=|a|=-a
几个二次根式化为最简二次根式后,如果被开方数相同,那么这几个二次根式就叫作同类二次根式。
合并同类二次根式,只需要将系数相加减,根指数和被开方数不变。
(2)二次根式的加减
①实质:
二次根式加减的实质是合并同类二次根式,例如
a√m+b√m=(a+b)√m
a√m-b√m=(a-b)√m
②步骤:
首先将每个二次根式都化简为最简二次根式,然后判断哪些二次根式是同类二次根式,再将同类二次根式系数相加减。
两个二次根式相乘,把被开方数相乘,根指数不变,如:√a·√b=√ab (a≥0)(b>0)。
(2)除法法则
两个二次根式相除,把被开方数相除,指数不变,如: =(a≥0)(b>0)。
=(a≥0)(b>0)。
有关二次根式的知识就整理到这里,通过迅捷思维导图工具,只需简单几步就可以轻松绘制出二次根式思维导图,小伙伴们也可以试着用思维导图整理其他知识点。

一、什么是二次根式思维导图
二次根式是指形如√a的代数表达式,其中a为非负实数。二次根式在数学中扮演着重要的角色,可以应用于代数、几何等多个数学领域。在思维导图中,我们可以将二次根式的概念作为中心节点,然后根据不同的性质,划分出各个分支。比如,可以有一个分支表示二次根式的简化方法,另一个分支表示二次根式的加减法则,还可以有一个分支表示二次根式的乘除法则等等。通过这样的思维导图,我们可以清晰地了解二次根式的各个方面,更好地应用于实际问题的解决过程中。
二、二次根式思维导图的重要性
二次根式思维导图的重要性体现在以下几个方面:1.清晰的结构化信息:
思维导图以图形化的方式展示了二次根式的各个概念和关系。通过将重要概念、定义、公式和解题方法等有机地组织起来,可以帮助学生更清晰地理解和记忆二次根式的知识。2.统一的知识框架:
思维导图可以形成一个统一的知识框架,将二次根式相关的内容串联起来。学生可以在思维导图中追溯相应知识点的来源和发展,从而更好地理解二次根式的内在逻辑。3.提高学习效率:
思维导图能够帮助学生快速回顾和复习二次根式的知识。通过浏览思维导图,学生可以迅速找到需要的信息,减少了查找资料的时间,提高了学习效率。
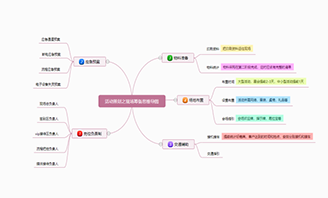
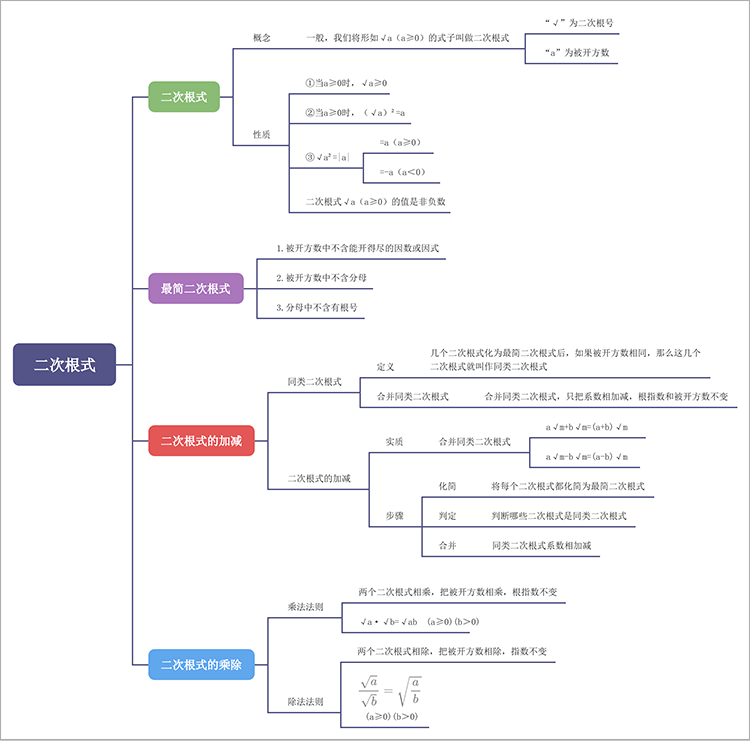
三、二次根式思维导图整理
1.二次根式
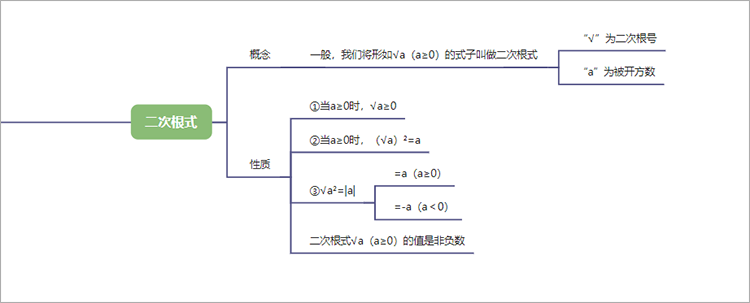
(1)概念:一般,我们将形如√a(a≥0)的式子叫做二次根式,其中“√”为二次根号,“a”为被开方数。(2)性质:
①当a≥0时,√a≥0
②当a≥0时,(√a)²=a
③当a≥0时,√a²=|a|=a
④当a<0时,√a²=|a|=-a

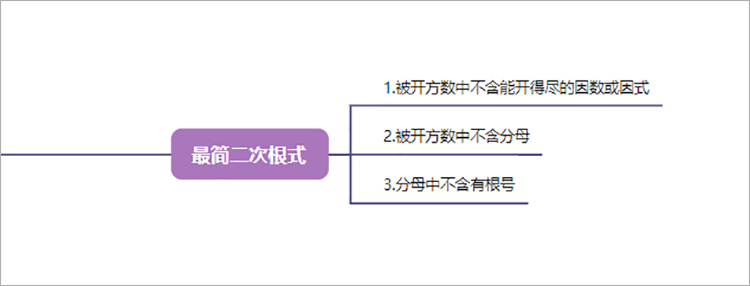
2.最简二次根式
最简二次根式中被开方数中不含能开得尽的因数或因式,且被开方数中不含分母、分母中不含有根号。
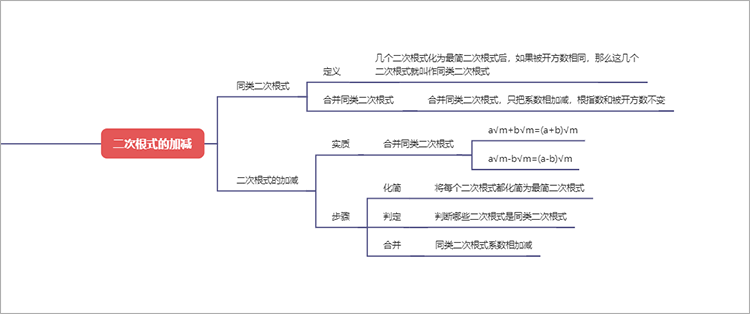
3.二次根式的加减
(1)同类二次根式几个二次根式化为最简二次根式后,如果被开方数相同,那么这几个二次根式就叫作同类二次根式。
合并同类二次根式,只需要将系数相加减,根指数和被开方数不变。
(2)二次根式的加减
①实质:
二次根式加减的实质是合并同类二次根式,例如
a√m+b√m=(a+b)√m
a√m-b√m=(a-b)√m
②步骤:
首先将每个二次根式都化简为最简二次根式,然后判断哪些二次根式是同类二次根式,再将同类二次根式系数相加减。

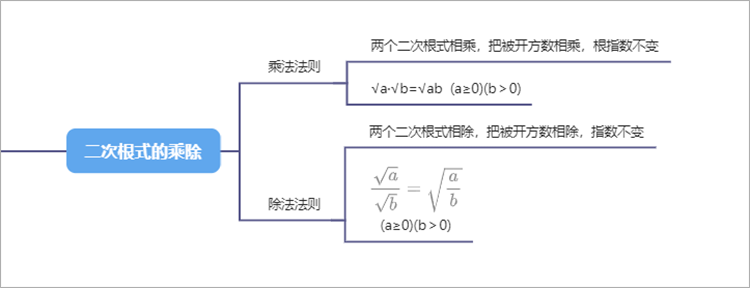
4.二次根式的乘除
(1)乘法法则两个二次根式相乘,把被开方数相乘,根指数不变,如:√a·√b=√ab (a≥0)(b>0)。
(2)除法法则
两个二次根式相除,把被开方数相除,指数不变,如:
 =(a≥0)(b>0)。
=(a≥0)(b>0)。
有关二次根式的知识就整理到这里,通过迅捷思维导图工具,只需简单几步就可以轻松绘制出二次根式思维导图,小伙伴们也可以试着用思维导图整理其他知识点。