认识三角形和四边形思维导图，让几何学习更加直观

2024-11-28 11:36:27 标签：思维导图

在几何学习中，三角形和四边形是两个最基础也是最重要的图形。它们不仅是几何学的基本构件，更是理解更复杂几何结构的基石。传统的学习方式往往依赖于文字和公式，容易造成学生对图形的抽象化理解，从而难以真正掌握其特性和应用。
为了让学生更直观地理解这些几何体，可以使用思维导图的工具，绘制认识三角形和四边形思维导图，将三角形和四边形的特征、性质及其相互关系可视化，使几何学习变得更加生动、有趣。

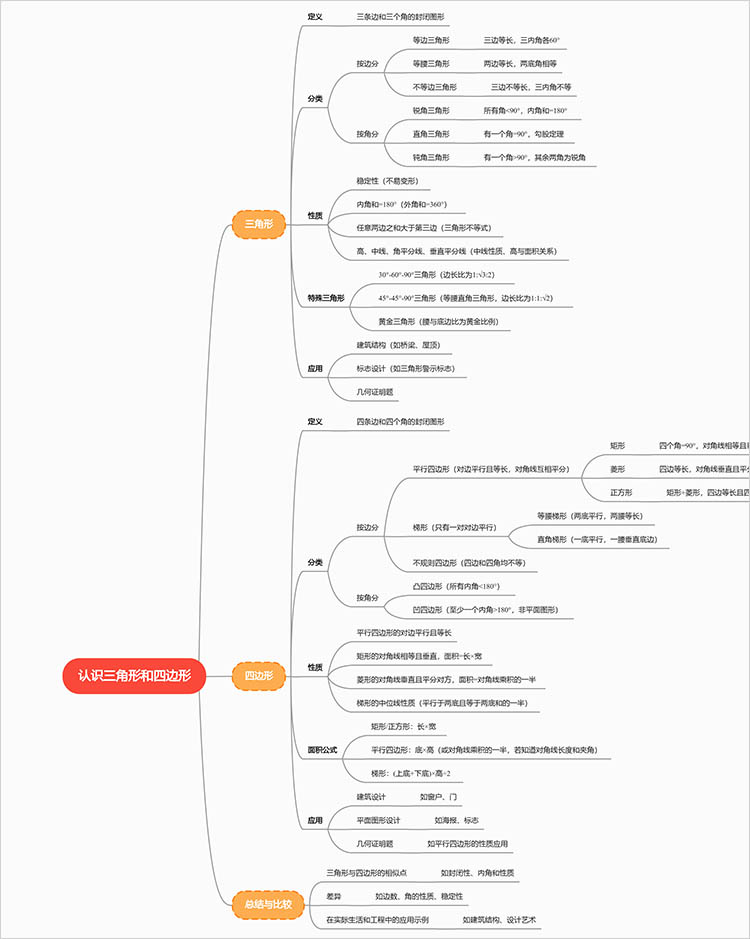
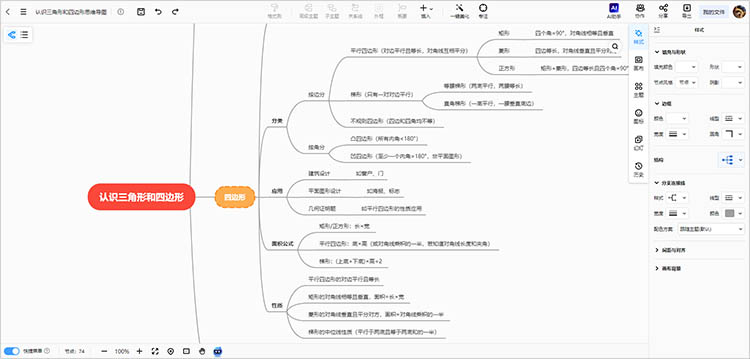
一、三角形的基本概念

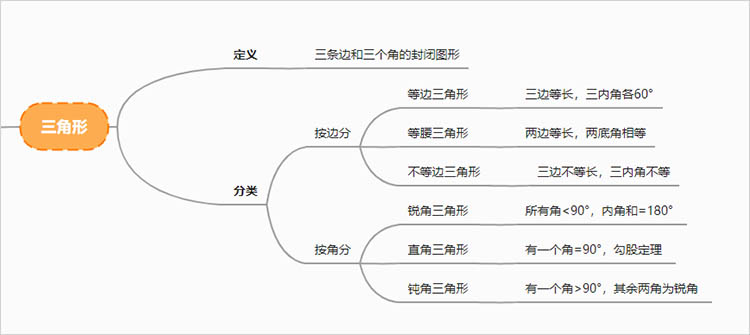
1.三角形的定义及分类

三角形，是由三条线段所围成的多边形。根据角的大小，可以将三角形分为锐角三角形、直角三角形和钝角三角形；根据边的长度，则可分为等边三角形、等腰三角形和不等边三角形。这些分类不仅有助于学生对三角形的理解，也为后续的几何证明和计算打下基础。

2.三角形的性质

三角形的内角和为180度，是一个核心定理。此外，三角形的外角等于不相邻内角之和等性质，使学生对角度的理解更加深刻；而边长的不等式定理则引导学生探讨几何形状之间的关系。

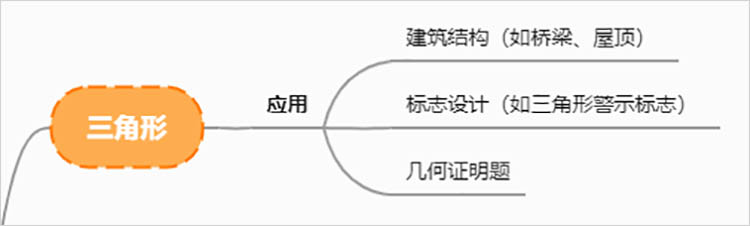
3.三角形在实际应用中的重要性

三角形作为建筑和工程设计中的基本单元，其稳定性和力学特性使其在各种结构中均扮演着重要角色。这种实际应用，不仅增强了学生的学习动机，也使几何学习与现实生活紧密相连。

二、四边形的基本概念

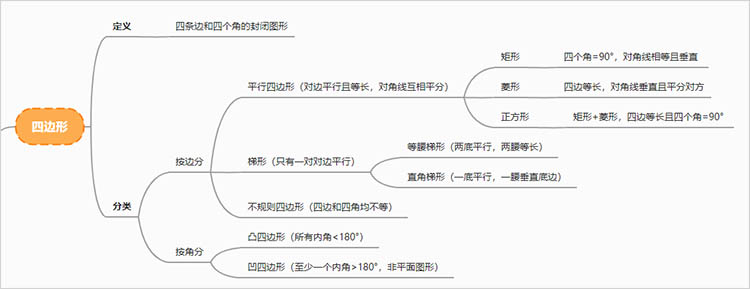
1.四边形的定义及分类

四边形是由四条线段围成的平面图形，常见的有矩形、正方形、平行四边形、梯形等。四边形的多样性使得它们在几何学习中成为重要的研究对象，通过对不同四边形的性质和特点的学习，学生能够更加深入地理解平面几何。

2.四边形的性质

各类四边形的性质各不相同，而它们之间的相互关系更是学习的重中之重。例如，矩形的对边平行且相等，内角均为90度，而正方形则是矩形的一种特殊情况。通过这些性质的理解，学生可以探索和证明不同类型四边形的特征。

3.四边形在实际应用中的重要性

在建筑设计和城市规划中，四边形形状的使用极为广泛。例如，房屋、窗户和道路设计中，很多结构都建立在四边形的基础上。理解这些形状的几何性质，对学生未来在这些领域的应用能力形成重要支撑。

三、思维导图在几何学习中的应用

1.思维导图的优势

思维导图作为一种有效的信息组织工具，能够将复杂的信息简化为清晰的结构，帮助学生系统地掌握知识点。通过在思维导图中将三角形和四边形的性质、分类和应用联系在一起，学生不仅能够更直观地理解几何知识，还能在考试和实际应用中灵活运用。

2.迅捷画图的功能

迅捷画图作为一款优秀的绘图工具，凭借其简单易用的界面和强大的功能，极大地方便了学生和教师进行几何图形的绘制。用户可以利用迅捷画图快速勾勒出各种几何形状，并标注出相应的性质。借助这个工具，思维导图的构建变得更加生动有趣，同时也激发了学生的创造力和学习兴趣。

3.构建三角形和四边形思维导图的步骤

使用迅捷画图构建思维导图的过程包括以下几个步骤：
①明确主题：选定三角形或四边形为主题，作为思维导图的中心节点。
②分类分支：按不同的性质和特点搭建分支，例如三角形的种类、性质，四边形的性质等。
③加入示例：在每个分支下加入具体示例，包括图形的绘制和性质说明，以加强对知识的理解。
④反馈与调整：通过与同学讨论和教师的反馈，对思维导图进行进一步的调整和完善。