实数思维导图,数学实数思维导图合集整理
2024-12-02 11:24:42
实数是数学中的一个重要概念,它是有理数和无理数的总称,涉及到数学中的许多章节和知识点。通过使用思维导图来整理实数的知识点,可以更好地理解和掌握实数的概念和性质,是一个很好的工具。本文下面我就分享数学实数思维导图合集,以及教大家如何绘制出简单的实数思维导图梳理图的方法。

首先,让我们来看下实数的分类。实数是指包括有理数和无理数在内的所有可以在数轴上一一对应的数字。实数包括有理数和无理数,它们都可以表示为有限位数或者无限位数的小数。
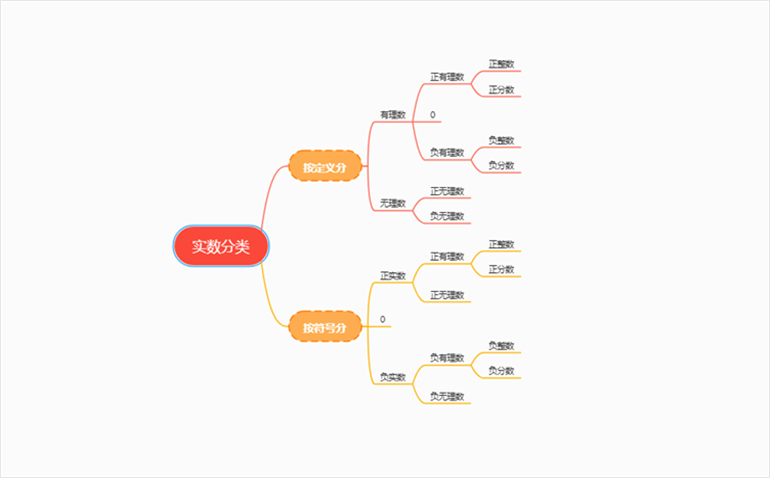
有理数是指可以表示为两个整数之比的数,即分母不为零的分数。例如,1/2、-3/4、5/1都是有理数。有理数包括正整数、负整数、零以及正分数、负分数。

无理数是指不能表示为两个整数之比的数,即不能写成分数的数。例如,根号2、圆周率π、自然常数e都是无理数。在数学中,无理数是有理数的补集,是一类与有理数截然不同的数。无理数在数学中有着广泛的应用,如几何、解析数论、数学分析等。

概念:—般地,如果一个数X的平方等于a,即x2=a,那么这个数x就叫做a的平方根(或二次方根)。
性质:一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根。
开平方求一个数a的平方根的运算,叫做开平方。

概念:—般地,如果一个数x的立方等于a,即x3=a,那么这个数號叫做a的立方根(或三次方根)。
性质:一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。

通过使用思维导图来整理实数的知识点,可以帮助我们更好地理解和掌握实数的概念和性质。同时,思维导图还可以帮助我们梳理知识点之间的联系和关系,从而提高我们的学习效率。
当我们把数学实数的基本知识梳理完后,后面就可以把大概简单内容汇总到思维导图中去。由于思维导图有着“分散性”的特点,我们就以层层递进的方式围绕主题中心(实数分类)进行扩展即可。
1、先从迅捷画图新建思维导图进入编辑页面;
2、以层层递进的方式将实数知识内容梳理至节点;
3、利用主题、图标、概要、公式等功能进一步完善内容;
4、将制作好的实数思维导图导出为PNG、PDF、WORD等格式。
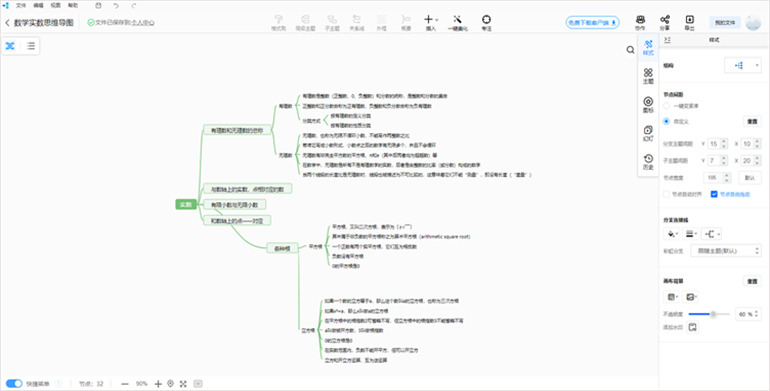
备注:大家要是创建思维导图时没有思路,可以在迅捷画图的模板库里寻找灵感,值得一提的是,还可以通过“协作”功能邀请他人与自己共同梳理并编辑数学实数思维导图。
总的来说,思维导图不仅可以帮助我们更好地理解数学知识,而且也能够提高我们的记忆力和思考能力。在学习过程中,大家可以根据自己的需要,在迅捷画图上制作适合自己的思维导图,提高自身学习效率。

首先,让我们来看下实数的分类。实数是指包括有理数和无理数在内的所有可以在数轴上一一对应的数字。实数包括有理数和无理数,它们都可以表示为有限位数或者无限位数的小数。

得知实数是由有理数和无理数组成之后,接下来就来具体了解下该两者之间的具体定义:
(1)有理数
有理数是指可以表示为两个整数之比的数,即分母不为零的分数。例如,1/2、-3/4、5/1都是有理数。有理数包括正整数、负整数、零以及正分数、负分数。

(2)无理数
无理数是指不能表示为两个整数之比的数,即不能写成分数的数。例如,根号2、圆周率π、自然常数e都是无理数。在数学中,无理数是有理数的补集,是一类与有理数截然不同的数。无理数在数学中有着广泛的应用,如几何、解析数论、数学分析等。

接下来,让我们来看一下在实数的计算方面,实数的运算会接触到平方根和立方根。
1、平方根
概念:—般地,如果一个数X的平方等于a,即x2=a,那么这个数x就叫做a的平方根(或二次方根)。
性质:一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根。
开平方求一个数a的平方根的运算,叫做开平方。

2、立方根
概念:—般地,如果一个数x的立方等于a,即x3=a,那么这个数號叫做a的立方根(或三次方根)。
性质:一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。

通过使用思维导图来整理实数的知识点,可以帮助我们更好地理解和掌握实数的概念和性质。同时,思维导图还可以帮助我们梳理知识点之间的联系和关系,从而提高我们的学习效率。
如何绘制实数思维导图?
当我们把数学实数的基本知识梳理完后,后面就可以把大概简单内容汇总到思维导图中去。由于思维导图有着“分散性”的特点,我们就以层层递进的方式围绕主题中心(实数分类)进行扩展即可。
1、先从迅捷画图新建思维导图进入编辑页面;
2、以层层递进的方式将实数知识内容梳理至节点;
3、利用主题、图标、概要、公式等功能进一步完善内容;
4、将制作好的实数思维导图导出为PNG、PDF、WORD等格式。

备注:大家要是创建思维导图时没有思路,可以在迅捷画图的模板库里寻找灵感,值得一提的是,还可以通过“协作”功能邀请他人与自己共同梳理并编辑数学实数思维导图。

总的来说,思维导图不仅可以帮助我们更好地理解数学知识,而且也能够提高我们的记忆力和思考能力。在学习过程中,大家可以根据自己的需要,在迅捷画图上制作适合自己的思维导图,提高自身学习效率。