用思维导图学习二元一次方程（组），通过思维导图整理知识点
2021-03-23 11:30:01
数学对于很多小伙伴来说是难以言说的痛，二元一次方程组是初中数学较为重要的知识点之一，为一些数学知识提供了铺垫，也可以用来解决部分生活中遇到的实际问题。其中思维导图作为思维辅助工具之一，可以用来整理归纳知识点，帮助我们理清思路，从而提高学习效率，然而我们该如何通过思维导图学习二元一次方程组呢？
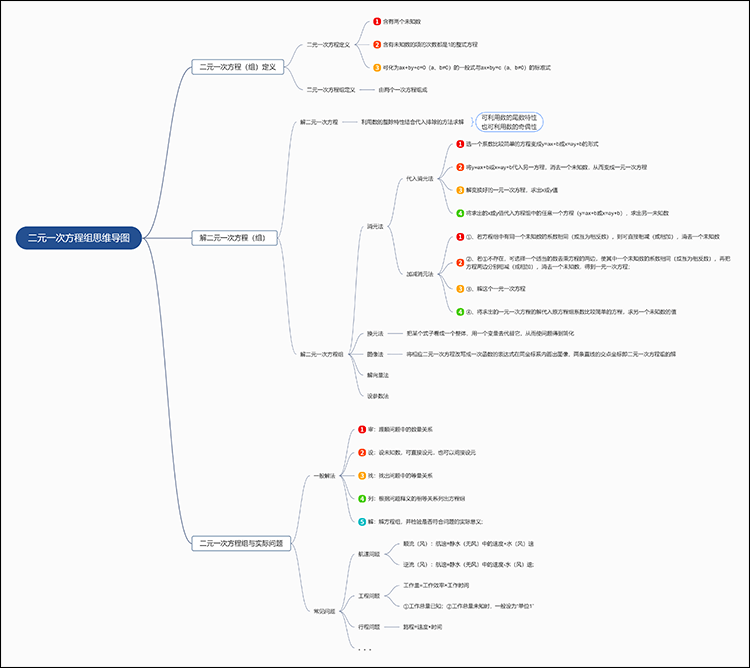
1、二元一次方程（组）定义
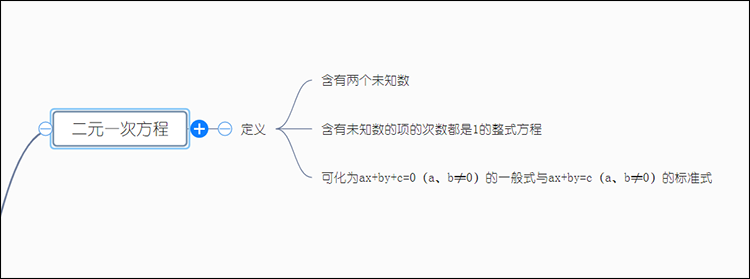
接着可以从简至难对思维导图的内容进行填充和完善，例如二元一次方程的成立需要满足三个条件：
（1）含有两个未知数；
（2）含有未知数的项的次数都是1的整式方程；
（3）可化为ax+by+c=0（a、b≠0）的一般式与ax+by=c（a、b≠0）的标准式。
接着将这些有关二元一次方程的成立条件（定义）填充至对应层级。
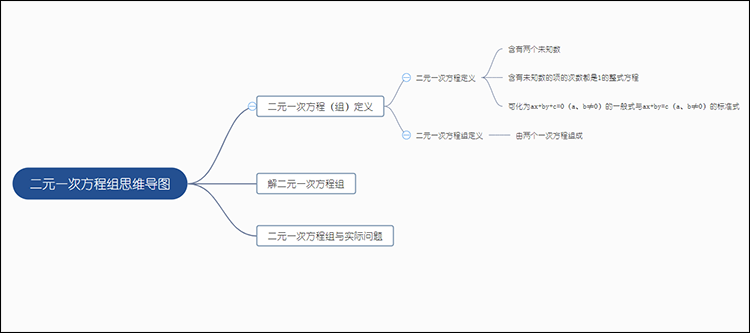
思维导图的制作是灵活的，当我们发现有更好表达内容的方式时可以作出相应的变通及调整，例如在总结二元一次方程定义时，还可以将二元一次方程组定义一并总结出来，但要注意两者之间的层级关系。
2、解二元一次方程（组）
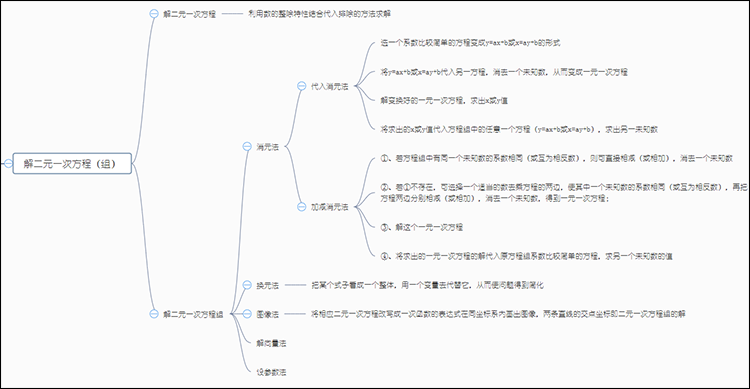
解二元一次方程的方式有一种：利用数的整除特性结合代入排除的方法求解。
解二元一次方程组的方式包含：消元法、换元法、设参数法、图像法、解向量法。
3、二元一次方程组解实际问题
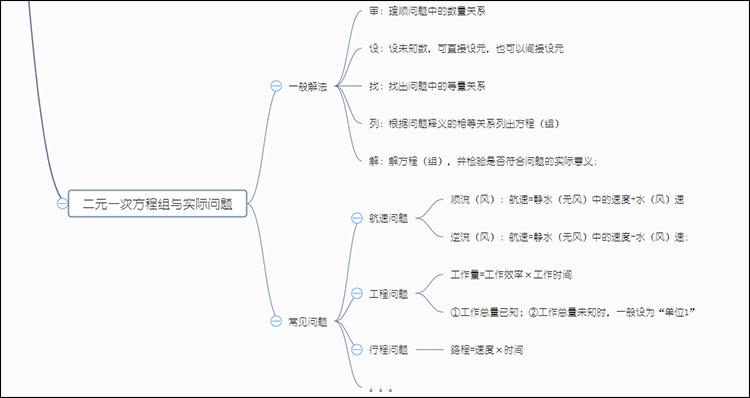
利用二元一次方程组解实际问题时，一般需要理清问题中的数量关系，接着根据已知内容设未知数，并从问题中找出存在的等量关系，而后根据这些内容中的相等关系列出方程组，解出方程组后检验答案是否符合问题中的实际意义。
二元一次组在实际问题中一般应用于解决航速问题、工程问题、形成问题等。
以上就是二元一次方程组思维导图的制作方法，思维导图可以很好地表达出绘制者的思路及想法，而每个人的思路及想法都有一定的差异，因此可以根据自己的思路进行总结。
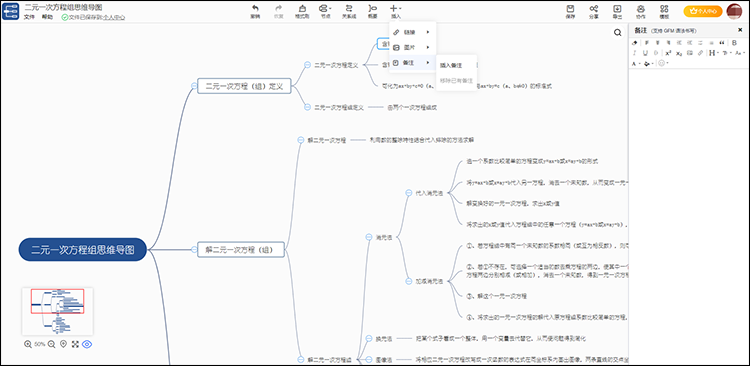
为了更好地完善及理解二元一次方程组的内容，通常可以附加上一些实际案例加以说明，而迅捷思维导图中可以给节点加上图片、链接及备注等素材，其中添加备注更是支持GFM语法书写。
2、插入图标
对于思维导图中一些有先后顺序的内容，可以通过“图标”加入优先级注明顺序，亦或对于重要内容还可以用不同“旗帜”或“星”加以说明。
3、插入概要
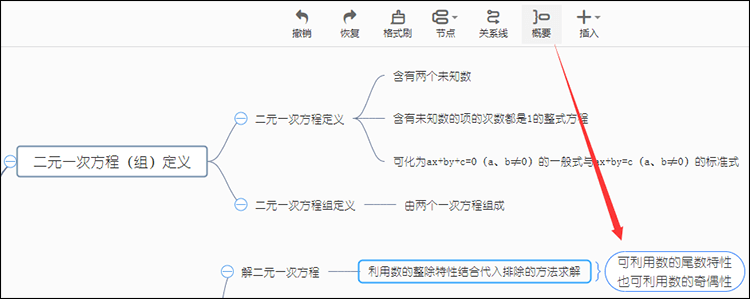
制作思维导图时经常需要对某个或某些内容做出更加详细的描述，可以利用概述功能加以说明。例如解二元一次方程中利用数的整除特性结合代入排除的方法求解--可利用数的尾数特性，也可利用数的奇偶性。
2、数据云存储：迅捷思维导图支持自动保存制作好的二元一次方程组思维导图，并将数据存储到云端，方便更换设备查看。
3、模板丰富：诸多行业的分类模板为制作思维导图提供思路。
4、多人协同：迅捷思维导图支持添加协作者，邀请他人一同绘制二元一次方程组思维导图，共同填充内容。
1.1. 二元一次方程（组）定义
1.1.1. 二元一次方程定义
1.1.1.1. 含有两个未知数
1.1.1.2. 含有未知数的项的次数都是1的整式方程
1.1.1.3. 可化为ax+by+c=0（a、b≠0）的一般式与ax+by=c（a、b≠0）的标准式
1.1.2. 二元一次方程组定义
1.1.2.1. 由两个一次方程组成
1.2. 解二元一次方程（组）
1.2.1. 解二元一次方程
1.2.1.1. 利用数的整除特性结合代入排除的方法求解
1.2.2. 解二元一次方程组
1.2.2.1. 消元法
1.2.2.1.1. 代入消元法
1.2.2.1.1.1. 选一个系数比较简单的方程变成y=ax+b或x=ay+b的形式
1.2.2.1.1.2. 将y=ax+b或x=ay+b代入另一方程，消去一个未知数，从而变成一元一次方程
1.2.2.1.1.3. 解变换好的一元一次方程，求出x或y值
1.2.2.1.1.4. 将求出的x或y值代入方程组中的任意一个方程（y=ax+b或x=ay+b），求出另一未知数
1.2.2.1.2. 加减消元法
1.2.2.1.2.1. ①、若方程组中有同一个未知数的系数相同（或互为相反数），则可直接相减（或相加），消去一个未知数
1.2.2.1.2.2. ②、若①不存在，可选择一个适当的数去乘方程的两边，使其中一个未知数的系数相同（或互为相反数），再把
方程两边分别相减（或相加），消去一个未知数，得到一元一次方程；
1.2.2.1.2.3. ③、解这个一元一次方程
1.2.2.1.2.4. ④、将求出的一元一次方程的解代入原方程组系数比较简单的方程，求另一个未知数的值
1.2.2.2. 换元法
1.2.2.2.1. 把某个式子看成一个整体，用一个变量去代替它，从而使问题得到简化
1.2.2.3. 图像法
1.2.2.3.1. 将相应二元一次方程改写成一次函数的表达式在同坐标系内画出图像，两条直线的交点坐标即二元一次方程组的解
1.2.2.4. 解向量法
1.2.2.5. 设参数法
1.3. 二元一次方程组解实际问题
1.3.1. 一般解法
1.3.1.1. 审：理顺问题中的数量关系
1.3.1.2. 设：设未知数，可直接设元，也可以间接设元
1.3.1.3. 找：找出问题中的等量关系
1.3.1.4. 列：根据问题释义的相等关系列出方程组
1.3.1.5. 解：解方程组，并检验是否符合问题的实际意义;
1.3.2. 常见问题
1.3.2.1. 航速问题
1.3.2.1.1. 顺流（风）：航速=静水（无风）中的速度+水（风）速
1.3.2.1.2. 逆流（风）：航速=静水（无风）中的速度-水（风）速;
1.3.2.2. 工程问题
1.3.2.2.1. 工作量=工作效率×工作时间
1.3.2.2.2. ①工作总量已知；②工作总量未知时，一般设为“单位1”
1.3.2.3. 行程问题
1.3.2.3.1. 路程=速度×时间
1.3.2.4. 。。。
一、二元一次方程组思维导图怎么画
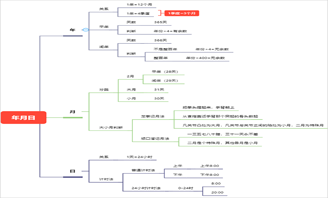
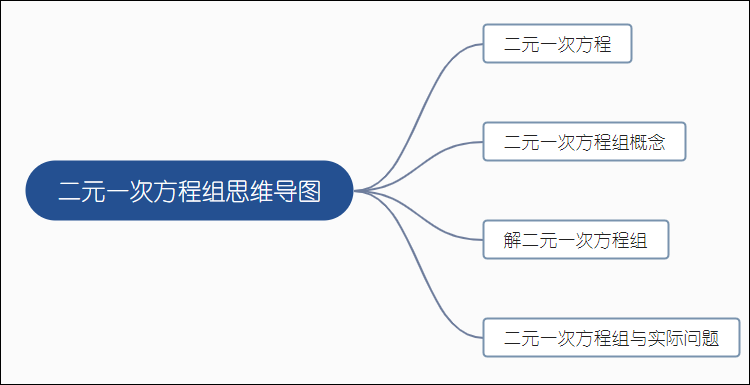
制作二元一次方程思维导图时，首先可以理顺整体制作大纲，例如可以将思维导图分为二元一次方程、二元一次方程组概念、解二元一次方程组、二元一次方程组解实际问题等多个部分。
接着可以从简至难对思维导图的内容进行填充和完善，例如二元一次方程的成立需要满足三个条件：
（1）含有两个未知数；
（2）含有未知数的项的次数都是1的整式方程；
（3）可化为ax+by+c=0（a、b≠0）的一般式与ax+by=c（a、b≠0）的标准式。
接着将这些有关二元一次方程的成立条件（定义）填充至对应层级。
解二元一次方程的方式有一种：利用数的整除特性结合代入排除的方法求解。
解二元一次方程组的方式包含：消元法、换元法、设参数法、图像法、解向量法。
利用二元一次方程组解实际问题时，一般需要理清问题中的数量关系，接着根据已知内容设未知数，并从问题中找出存在的等量关系，而后根据这些内容中的相等关系列出方程组，解出方程组后检验答案是否符合问题中的实际意义。
二元一次组在实际问题中一般应用于解决航速问题、工程问题、形成问题等。
二、二元一次方程组思维导图制作技巧
1、插入素材为了更好地完善及理解二元一次方程组的内容，通常可以附加上一些实际案例加以说明，而迅捷思维导图中可以给节点加上图片、链接及备注等素材，其中添加备注更是支持GFM语法书写。
对于思维导图中一些有先后顺序的内容，可以通过“图标”加入优先级注明顺序，亦或对于重要内容还可以用不同“旗帜”或“星”加以说明。
制作思维导图时经常需要对某个或某些内容做出更加详细的描述，可以利用概述功能加以说明。例如解二元一次方程中利用数的整除特性结合代入排除的方法求解--可利用数的尾数特性，也可利用数的奇偶性。
三、为什么要用迅捷画图制作二元一次方程组思维导图？
1、多平台制作：迅捷思维导图支持在线和软件制作，其中在线制图方式可在Windows、mac等设备的浏览器中使用。2、数据云存储：迅捷思维导图支持自动保存制作好的二元一次方程组思维导图，并将数据存储到云端，方便更换设备查看。
3、模板丰富：诸多行业的分类模板为制作思维导图提供思路。
4、多人协同：迅捷思维导图支持添加协作者，邀请他人一同绘制二元一次方程组思维导图，共同填充内容。
四、二元一次方程组思维导图大纲
1. 二元一次方程组思维导图1.1. 二元一次方程（组）定义
1.1.1. 二元一次方程定义
1.1.1.1. 含有两个未知数
1.1.1.2. 含有未知数的项的次数都是1的整式方程
1.1.1.3. 可化为ax+by+c=0（a、b≠0）的一般式与ax+by=c（a、b≠0）的标准式
1.1.2. 二元一次方程组定义
1.1.2.1. 由两个一次方程组成
1.2. 解二元一次方程（组）
1.2.1. 解二元一次方程
1.2.1.1. 利用数的整除特性结合代入排除的方法求解
1.2.2. 解二元一次方程组
1.2.2.1. 消元法
1.2.2.1.1. 代入消元法
1.2.2.1.1.1. 选一个系数比较简单的方程变成y=ax+b或x=ay+b的形式
1.2.2.1.1.2. 将y=ax+b或x=ay+b代入另一方程，消去一个未知数，从而变成一元一次方程
1.2.2.1.1.3. 解变换好的一元一次方程，求出x或y值
1.2.2.1.1.4. 将求出的x或y值代入方程组中的任意一个方程（y=ax+b或x=ay+b），求出另一未知数
1.2.2.1.2. 加减消元法
1.2.2.1.2.1. ①、若方程组中有同一个未知数的系数相同（或互为相反数），则可直接相减（或相加），消去一个未知数
1.2.2.1.2.2. ②、若①不存在，可选择一个适当的数去乘方程的两边，使其中一个未知数的系数相同（或互为相反数），再把
方程两边分别相减（或相加），消去一个未知数，得到一元一次方程；
1.2.2.1.2.3. ③、解这个一元一次方程
1.2.2.1.2.4. ④、将求出的一元一次方程的解代入原方程组系数比较简单的方程，求另一个未知数的值
1.2.2.2. 换元法
1.2.2.2.1. 把某个式子看成一个整体，用一个变量去代替它，从而使问题得到简化
1.2.2.3. 图像法
1.2.2.3.1. 将相应二元一次方程改写成一次函数的表达式在同坐标系内画出图像，两条直线的交点坐标即二元一次方程组的解
1.2.2.4. 解向量法
1.2.2.5. 设参数法
1.3. 二元一次方程组解实际问题
1.3.1. 一般解法
1.3.1.1. 审：理顺问题中的数量关系
1.3.1.2. 设：设未知数，可直接设元，也可以间接设元
1.3.1.3. 找：找出问题中的等量关系
1.3.1.4. 列：根据问题释义的相等关系列出方程组
1.3.1.5. 解：解方程组，并检验是否符合问题的实际意义;
1.3.2. 常见问题
1.3.2.1. 航速问题
1.3.2.1.1. 顺流（风）：航速=静水（无风）中的速度+水（风）速
1.3.2.1.2. 逆流（风）：航速=静水（无风）中的速度-水（风）速;
1.3.2.2. 工程问题
1.3.2.2.1. 工作量=工作效率×工作时间
1.3.2.2.2. ①工作总量已知；②工作总量未知时，一般设为“单位1”
1.3.2.3. 行程问题
1.3.2.3.1. 路程=速度×时间
1.3.2.4. 。。。
