知识点归纳!人教版七年级下册数学思维导图分享
2021-04-21 18:42:42
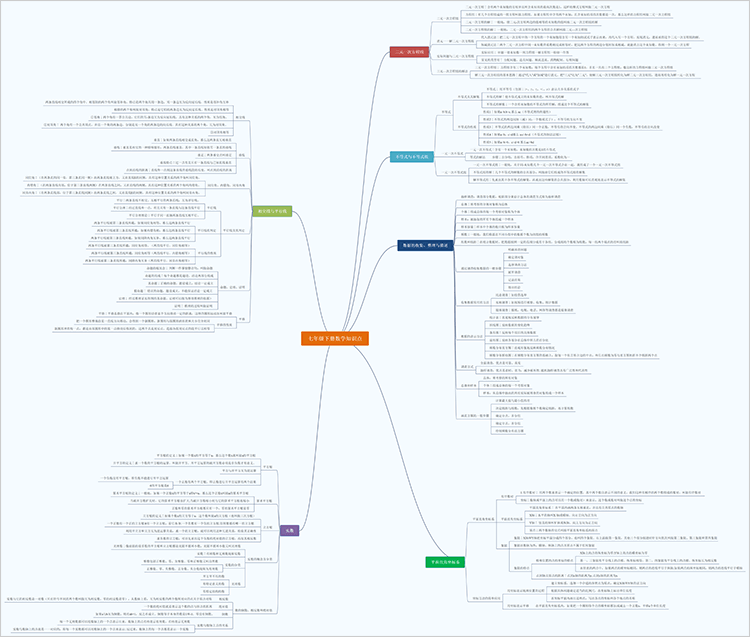
人教版七年级下册数学有六个章节,教导学生学习相交线与平行线、实数、平面直角坐标系、二元一次方程组、不等式与不等式组、数据的收集,整理与描述等知识内容。
由于人教版七年级下册数学的知识点繁多,不少同学在学习时容易出现知识点记忆混乱或知识点理解不清晰等问题。为此,我们可以将人教版七年级下册数学课文所包含的知识点总结并归纳至思维导图中,便于理解与体现其中的重点及难点内容。
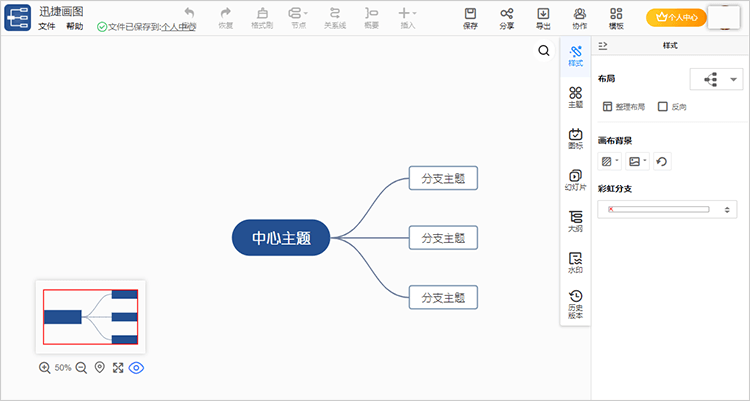
step2:接下来会进入到编辑页面,此时围绕人教版七年级下册数学知识点并结合思维导图简单画法从中心主题开始对内容进行延伸。
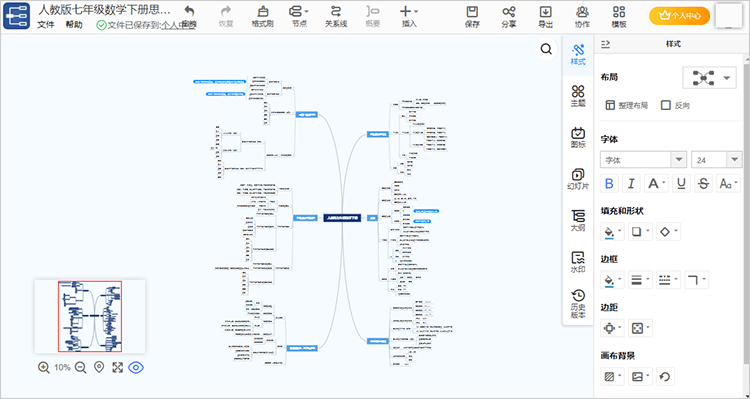
step3:除了简单延伸思维导图的节点外,还可以结合右侧工具栏的样式、主题、图标幻灯片、大纲、水印、历史版本等功能编辑节点样式,或以大纲等形式预览内容。
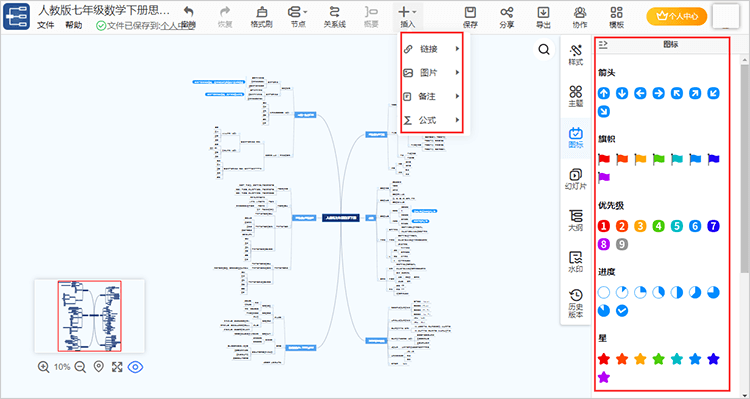
step4:编辑过程中注意其中的“图标”与“插入”功能,可以利用箭头、优先级、星等分类的图标突出知识点的重点及难点内容,或利用插入功能给节点添加参考链接、图片、备注、公式。
step5:人教版七年级下册数学知识点的内容总结归纳至思维导图后,将其“保存”至云端或“导出”为Word、PPT、PDF、PNG、JPG等格式保存至设备本地。
思维导图除了可以用来总结归纳人教版七年级下册数学知识点外,能做的还有很多,如常见场景有制定学习计划、会议纪要、读书笔记等。小伙伴们可以尝试着绘制哟!
2、数据云存储:迅捷思维导图支持自动保存制作好的人教版七年级下册数学思维导图,并将数据存储到云端,方便更换设备查看。
3、模板丰富:诸多行业的分类模板为制作思维导图提供思路。
4、多人协同:迅捷思维导图支持添加协作者,邀请他人一同绘制人教版七年级下册数学思维导图,共同填充内容。
1.1.1. 二元一次方程组
1.1.1.1. 二元一次方程∶含有两个未知数的方程并且所含未知项的最高次数是1,这样的整式方程叫做二元一次方程
1.1.1.2. 方程组∶有几个方程组成的一组方程叫做方程组。如果方程组中含有两个未知,且含未知的项的次数都是一次,那么这样的方程组叫做二元一次方程组
1.1.1.3. 二元一次方程的解∶ 一般地,使二元-次方程两边的值相等的未知数的值叫做二元一次方程组的解
1.1.1.4. 二元一次方程组的解∶ 一般地,二元一次方程组的两个方程的公共解叫做二元—次方程组
1.1.2. 消元一一解二元一次方程组
1.1.2.1. 代入消元法∶把二元一次方程中的一个方程的一个未知数用含另一个未知的试式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。
1.1.2.2. 加减消元法∶两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程
1.1.3. 实际问题与二元一次方程组
1.1.3.1. 实际应用∶ 审题一设未知数一列方程组一解方程组一检验一作答
1.1.3.2. 常见的类型有∶ 分配问题、追及问题、顺流送流、药物配制、行程问题
1.1.4. 三元—次方程组的解法
1.1.4.1. 三元一次方程组∶ 方程组含有三个未知数,每个方程中含有未知的项的次数都是1,并且一共有三个方程组,像这样的方程组叫做三元一次方程组
1.1.4.2. 解三元一次方程组的基本思路∶通过"代入"或"加减"进行消元。把"三元"化为"二元",使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程
1.2. 不等式与不等式组
1.2.1. 不等式
1.2.1.1. 不等式及其解集
1.2.1.1.1. 不等式∶ 用不等号(包括∶>、≥、≤、<、≠)表示大小关系的式子
1.2.1.1.2. 不等式的解∶使不等式成立的未知数的值,叫不等式的解
1.2.1.1.3. 不等式的解集∶一个含有未知数的不等式的所有解,组成这个不等式的解集
1.2.1.2. 不等式的性质
1.2.1.2.1. 性质1∶如果a>b.b>c.那么 ac(不等式增的传递性)
1.2.1.2.2. 性质2∶不等式的两边同加(减)同-一个数或式子),不等号的方向不变
1.2.1.2.3. 性质3∶ 不等式的两边同乘(除以)同一个正数,不等号的方向不变。不等式的两边同乘(除以)同一个负数,不等号的方向改变
1.2.1.2.4. 性质4∶如果a>b,c>d那么 a-c>b+d.(不等式的加法法则)
1.2.1.2.5. 性质5∶如果a>b>0,c>d>0.那么ac>bd
1.2.2. 一元一次不等式
1.2.2.1. 一元一次不等式∶含有一个未知数,未知数的次数是1的不等式
1.2.2.2. 等式的解法
1.2.2.2.1. 步骤∶去分母,去括号,移项,合并同类项,系数化为一
1.2.3. 一元一次不等式组
1.2.3.1. 一元一次不等式组∶一般地,关于同-未知数几个一元一次不等式合在一起,就组成了一个一元一次不等式组
1.2.3.2. 不等式组的解∶几个不等式的解集的公共部分,叫做由它们组成的不等式组的解集
1.2.3.3. 解不等式组∶先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式的解集
1.3. 数据的收集、整理与描述
1.3.1. 抽样调查:调查部分数据,根据部分来估计总体的调查方式称为抽样调查
1.3.2. 总体∶要考察的全体对象称为总体
1.3.3. 个体∶组成总体的每一个考察对象称为个体
1.3.4. 样本:被抽取的所有个体组成一个样本
1.3.5. 样本容量∶样本中个体的数目称为样本客量
1.3.6. 频数∶一般地,我们称落在不同小组中的数据个数为该组的频数
1.3.7. 组数和组距∶在统计数据时,把数据按照一定的范围分成若干各组,分成组的个数称为组数,每一组两个端点的差叫做组距
1.3.8. 通过调查收集数据的一般步骤
1.3.8.1. 明确周查问题
1.3.8.2. 确定调对象
1.3.8.3. 选择调查方法
1.3.8.4. 展开调查
1.3.8.5. 记录结果
1.3.8.6. 得出结论
1.3.9. 收集数据常用的方法
1.3.9.1. 民意调查∶如投票选举
1.3.9.2. 实地调查∶如现场进行观察、收集、统计数据
1.3.9.3. 媒体调查∶报纸、电视、电话、网络等调查都是媒体调查
1.3.10. 数据的表示方法
1.3.10.1. 统计表∶直观地反映数据的分布规律
1.3.10.2. 折线图∶反映数据的变化趋势
1.3.10.3. 条形图∶反映每个项目的具体数据
1.3.10.4. 扇形图∶反映各部分在总体中所占的百分比
1.3.10.5. 频数分布直方图∶直观形象地反映频数分布情况
1.3.10.6. 频数分布折结图∶在频数分布直方图的基础上,取每一个长方形上边的中点,和左右频数为零与直方图相距半个组距两个点
1.3.11. 调查方式
1.3.11.1. 全面调查,优点是可靠、真实
1.3.11.2. 抽样调查,优点是省时、省力,减少破坏性; 随机抽样调查具有广泛性和代表性
1.3.12. 总体和样本
1.3.12.1. 总体:要考察的所有对象
1.3.12.2. 个体∶组成总体的每一个考察对象
1.3.12.3. 样本:从总体中抽出的所有实际被周查的对象组成一个样本
1.3.13. 画直方图的一般步骤
1.3.13.1. 计算最大值与最小值的差
1.3.13.2. 决定组距与组数,先根据数据个数确定组距,再计算组数
1.3.13.3. 确定分点,并分组
1.3.13.4. 确定分点,并分组
1.3.13.5. 绘制频数分布直方图
1.4. 相交线与平行线
1.4.1. 相交线
1.4.1.1. 两条直线相交所成的四个角中,相邻阳的两个角叫做邻补角,特点是两个角共用一条边,另一条边互为反向延长线,性质是邻补角互补
1.4.1.2. 相排的两个角叫做对顶角,特点是它们的两条边互为反向延长线。性质是对顶角相等
1.4.1.3. ①邻角∶两个角有一茶公共边,它们的另-条边互为反向延长线。具有这种关系的两个角,互为邻角。
1.4.1.4. ②对顶角∶ 两个角有一个公共顶点,并且一个角的两条边,分别是另一个角的两条边的向长线,具有这种关系的两个角,互为对顶角。
1.4.1.5. ③对顶角相等
1.4.2. 垂线
1.4.2.1. 垂直∶如果两条直线相交成直角,那么这两条直互相垂直
1.4.2.2. 垂线∶垂直是相交的一种特殊情形,两条直线垂直,其中一条直线知做另一条直的垂线
1.4.2.3. 垂足∶两条垂交点叫垂足
1.4.2.4. 垂线特点∶过一点有且只有一条直线与已知直线垂直
1.4.2.5. 点到直线的距离∶直线外一点到这条直线的垂线段的长度,叫点到直线的距离
1.4.3. 同位角、内错角、同旁内角
1.4.3.1. 同位角∶(在两条直的同一旁,第三条直同一侧)在两条直线谢上方,又在直线E的同侧,具有这种位置关系的两个角叫同位角。
1.4.3.2. 内错角∶(在两条直线内部,位于第三条直线两侧)在两条直线之间,又在直线的两侧,具有这种位置关系的两个角叫内错角。
1.4.3.3. 同旁内角∶(在两条直线部,位于第三条直线同测)在两条直线之间,又在直线E的同侧,具有这种位置关系的两个角叫同旁内角。
1.4.4. 平行线及其判定
1.4.4.1. 平行线
1.4.4.1.1. 平行∶两条直线不相交。互相平行的两条直线,互为评行线。
1.4.4.1.2. 平行公理∶经过直线外一点,有且只有一条直线与这条直线平行
1.4.4.1.3. 平行公理推论∶平行于同一直绨两条直线互相平行。
1.4.4.2. 平行线的判定
1.4.4.2.1. 两条平行线被第三条直线所截,如果同位角相等,那么这两条直线平行
1.4.4.2.2. 两条平行线被第三条直线所截,如果内错角相,那么这两条直线平行
1.4.4.2.3. 两条平行线被第三条直线所截,如果同降内角互补,那么这两条直线平行
1.4.4.3. 平行线的性质
1.4.4.3.1. 两条平行线被第三条直线所截,同位角相等。(两直线平行,同位角相等)
1.4.4.3.2. 两条平行线被第三条直线所截,同位角相等(两直线平行,内错角相等)
1.4.4.3.3. 两条平行线被第三条直线所截,同降内角互补(两直线平行,同旁内角相等)
1.4.5. 命题、定理、证明
1.4.5.1. 命题的辊况念∶ 判断一件事情骼语句,叫做命题
1.4.5.2. 命题的组成∶每个命题都是题设、结论两部分组成
1.4.5.3. 真命题∶正确的命题,题设成立,结论一定成立
1.4.5.4. 假命题∶ 错误的命题,题设成立,不能保证结论一定成立
1.4.5.5. 定理∶ 经过推理证实得到的真命题。定理可以做为继续推理的依据)
1.4.5.6. 证明∶ 推理的过程叫做证明
1.4.6. 平移
1.4.6.1. 平移∶平移是指在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动加叫做平移
1.4.6.2. 平移的性质
1.4.6.2.1. 把一个图形整体沿某一直线方向移动,会得到一个新图形,新图形与原图形纳形状和大小完全相同
1.4.6.2.2. 新图形冲的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点。连接各组对应点的段平行且相等
1.5. 实数
1.5.1. 平方根
1.5.1.1. 平方根的定义∶如果一个数x的平方等于a,那么这个数x就叫做a的平方根
1.5.1.2. 开平方的定义∶求一个数的平方根的运算,叫做开平方。开平方运算的被开方数必须是非负数才有意义。
1.5.1.3. 平方与开平方互为逆运算
1.5.1.4. 一个正数有两个平方根。即正数进行开平方运算有两个结果
1.5.1.4.1. 一个负数没有平方根,即负数不能进行开平方运算
1.5.1.4.2. 0的平方根是0
1.5.2. 算术平方根
1.5.2.1. 算术平方根的定义∶一般地,如果一个正数x的平方等于a即x²=a,那么这个正数x叫做a的算术平方根
1.5.2.2. 当被开方数扩太时,它的算术平方根也扩大;当被开方数缩小时与它的算术平方根也缩小
1.5.2.3. 正数和零的算术平方根都只有一个,零的算术平方根是零
1.5.3. 立方根
1.5.3.1. 立方根的定义∶如果个数x的立方等于a,这个数叫做a的立方根(也叫做三次方根)
1.5.3.2. 一个正数有一个正的立方根;0有一个立方根,是它本身;一个负数有一个负的立方根;任何数都有唯一的立方根
1.5.3.3. 利用开立方和立方互为逆运算关系,求一个的立方根,就可以利用这种互逆关系,检验其正确性
1.5.3.4. 求负数的立方根,可以先求出这个负数的绝对值的立方根,再取其相反数
1.5.4. 实数的概念及分类
1.5.4.1. 无理数∶像前面的很多数的平方根和立方根都是无限不循环小数,无限不循环小数又叫无理数
1.5.4.2. 实数∶有理数和无理数统称实数
1.5.4.3. 实数的分类
1.5.4.3.1. 整数包括正整数、零、负整数。零和正整数又叫自然数
1.5.4.3.2. 正整数、零、负整数、正分数、负分数统称为有理数
1.5.4.4. 无理数
1.5.4.4.1. 开方开不尽的数
1.5.4.4.2. 有特定意义的数
1.5.4.4.3. 有特定结构的数
1.5.5. 数的倒数、相反数和绝对值
1.5.5.1. 相反数
1.5.5.1.1. 实数与它的相反数是一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零),从数轴上看,互为相反数的两个数所对应的点关于原点对称
1.5.5.2. 绝对值
1.5.5.2.1. 一个数的绝对值就是表示这个数的点与原点的距离
1.5.5.3. 倒数
1.5.5.3.1. 如果a与b互为倒数,则有ab=1,反之亦成立。倒数等于本身的数是1和-1。零没有倒数。
1.5.5.4. 实数与数轴上点的关系
1.5.5.4.1. 每一个无理数都可以用数轴上的一个点表示出来,数轴上的点有些表示有理数,有些表示无理数
1.5.5.4.2. 实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的一个点来表示; 反过来,数轴上的每一个点都是表示一个实数
1.6. 平面直角坐标系
1.6.1. 平面直角坐标系
1.6.1.1. 有序数对
1.6.1.1.1. 1.有序数对∶ 用两个数来表示一个确定的位置,其中两个数自表示不同的意义,我们这种有顺序的两个数组成的数对,叫做有序数对
1.6.1.1.2. 坐标∶数轴或平面上的点可以用一个数或数对)来表示,这个数或数对叫做这个点的坐标
1.6.1.2. 平面直角坐标系
1.6.1.2.1. 平面直角坐标系∶ 在平面内画两条互相垂直,并且有公共原点的数轴
1.6.1.2.2. X轴∶水平的轴叫X 轴或横轴。向右方向为正方向
1.6.1.2.3. Y轴∶ 竖直的轴叫Y 轴或纵轴。向上方向为正方向
1.6.1.2.4. 原点∶两个数轴的交点叫做平面直角坐标系的原点
1.6.1.3. 象限
1.6.1.3.1. 象限∶X轴和Y轴把坐标平面分成四个部分,也叫四个象限。右上面做第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限
1.6.1.3.2. 象限以数轴为界,横轴、纵轴上的点及原点不属于任何象限
1.6.1.3.3. 象限的特点
1.6.1.3.3.1. 特殊位置的点的坐标的特点
1.6.1.3.3.1.1. X轴上的点的纵坐标为零;Y轴上的点的横坐标为零
1.6.1.3.3.1.2. 第一、三象限角平分线上的点横、纵坐标相等,第二、四象限角平分线上的点横、纵坐标互为相反数
1.6.1.3.3.1.3. 在任意的两点中,如果两点的横坐标相同,则两点的连线平行于纵轴;如果两点的纵坐标相同,则两点的连线平行于横轴
1.6.1.3.3.2. 点到轴及原点的距离∶点到x轴的距离为y;点到y轴的距离为x
1.6.2. 坐标方法的简单应用
1.6.2.1. 用坐标表示地理位置的过程
1.6.2.1.1. 建立坐标系,选择一个合适的参照点为原点,确定Ⅹ轴和Y轴的证方向
1.6.2.1.2. 根据具体问题确定适当的比例尺,在坐标轴上标出单位长度
1.6.2.1.3. 在坐标平面内画出这些点,写出各点的坐标和各个地点的名称
1.6.2.2. 用坐标表示平移
1.6.2.2.1. 在平面直角坐标系内,如果把一个图形络个点的横坐标都加或减去一个正数s,平移a个单位长度
由于人教版七年级下册数学的知识点繁多,不少同学在学习时容易出现知识点记忆混乱或知识点理解不清晰等问题。为此,我们可以将人教版七年级下册数学课文所包含的知识点总结并归纳至思维导图中,便于理解与体现其中的重点及难点内容。

好用的思维导图绘制软件
迅捷画图是一款好用的在线思维导图绘制工具,可以帮助你简单绘制人教版七年级下册数学思维导图,整理并归纳其中的知识点。这款在线软件除了简单的添加、删除、拖拽节点外,具有不少特色功能,如多人协作,插入格式、插入GFM语法书写的备注、插入节点关键线、插入节点概要等。人教版七年级下册数学思维导图怎么画
step1:进入迅捷画图在线网站新建空白思维导图(或在模板库中寻找一份合适的模板进行套用)。
step2:接下来会进入到编辑页面,此时围绕人教版七年级下册数学知识点并结合思维导图简单画法从中心主题开始对内容进行延伸。

step3:除了简单延伸思维导图的节点外,还可以结合右侧工具栏的样式、主题、图标幻灯片、大纲、水印、历史版本等功能编辑节点样式,或以大纲等形式预览内容。

step4:编辑过程中注意其中的“图标”与“插入”功能,可以利用箭头、优先级、星等分类的图标突出知识点的重点及难点内容,或利用插入功能给节点添加参考链接、图片、备注、公式。

step5:人教版七年级下册数学知识点的内容总结归纳至思维导图后,将其“保存”至云端或“导出”为Word、PPT、PDF、PNG、JPG等格式保存至设备本地。

思维导图除了可以用来总结归纳人教版七年级下册数学知识点外,能做的还有很多,如常见场景有制定学习计划、会议纪要、读书笔记等。小伙伴们可以尝试着绘制哟!
为什么要用迅捷画图制作人教版七年级下册数学思维导图?
1、多平台制作:迅捷思维导图支持在线和软件制作,其中在线制图方式可在Windows、mac等设备的浏览器中使用。2、数据云存储:迅捷思维导图支持自动保存制作好的人教版七年级下册数学思维导图,并将数据存储到云端,方便更换设备查看。
3、模板丰富:诸多行业的分类模板为制作思维导图提供思路。
4、多人协同:迅捷思维导图支持添加协作者,邀请他人一同绘制人教版七年级下册数学思维导图,共同填充内容。
七年级下册数学思维导图大纲
1.1. 二元一次方程组1.1.1. 二元一次方程组
1.1.1.1. 二元一次方程∶含有两个未知数的方程并且所含未知项的最高次数是1,这样的整式方程叫做二元一次方程
1.1.1.2. 方程组∶有几个方程组成的一组方程叫做方程组。如果方程组中含有两个未知,且含未知的项的次数都是一次,那么这样的方程组叫做二元一次方程组
1.1.1.3. 二元一次方程的解∶ 一般地,使二元-次方程两边的值相等的未知数的值叫做二元一次方程组的解
1.1.1.4. 二元一次方程组的解∶ 一般地,二元一次方程组的两个方程的公共解叫做二元—次方程组
1.1.2. 消元一一解二元一次方程组
1.1.2.1. 代入消元法∶把二元一次方程中的一个方程的一个未知数用含另一个未知的试式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。
1.1.2.2. 加减消元法∶两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程
1.1.3. 实际问题与二元一次方程组
1.1.3.1. 实际应用∶ 审题一设未知数一列方程组一解方程组一检验一作答
1.1.3.2. 常见的类型有∶ 分配问题、追及问题、顺流送流、药物配制、行程问题
1.1.4. 三元—次方程组的解法
1.1.4.1. 三元一次方程组∶ 方程组含有三个未知数,每个方程中含有未知的项的次数都是1,并且一共有三个方程组,像这样的方程组叫做三元一次方程组
1.1.4.2. 解三元一次方程组的基本思路∶通过"代入"或"加减"进行消元。把"三元"化为"二元",使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程
1.2. 不等式与不等式组
1.2.1. 不等式
1.2.1.1. 不等式及其解集
1.2.1.1.1. 不等式∶ 用不等号(包括∶>、≥、≤、<、≠)表示大小关系的式子
1.2.1.1.2. 不等式的解∶使不等式成立的未知数的值,叫不等式的解
1.2.1.1.3. 不等式的解集∶一个含有未知数的不等式的所有解,组成这个不等式的解集
1.2.1.2. 不等式的性质
1.2.1.2.1. 性质1∶如果a>b.b>c.那么 ac(不等式增的传递性)
1.2.1.2.2. 性质2∶不等式的两边同加(减)同-一个数或式子),不等号的方向不变
1.2.1.2.3. 性质3∶ 不等式的两边同乘(除以)同一个正数,不等号的方向不变。不等式的两边同乘(除以)同一个负数,不等号的方向改变
1.2.1.2.4. 性质4∶如果a>b,c>d那么 a-c>b+d.(不等式的加法法则)
1.2.1.2.5. 性质5∶如果a>b>0,c>d>0.那么ac>bd
1.2.2. 一元一次不等式
1.2.2.1. 一元一次不等式∶含有一个未知数,未知数的次数是1的不等式
1.2.2.2. 等式的解法
1.2.2.2.1. 步骤∶去分母,去括号,移项,合并同类项,系数化为一
1.2.3. 一元一次不等式组
1.2.3.1. 一元一次不等式组∶一般地,关于同-未知数几个一元一次不等式合在一起,就组成了一个一元一次不等式组
1.2.3.2. 不等式组的解∶几个不等式的解集的公共部分,叫做由它们组成的不等式组的解集
1.2.3.3. 解不等式组∶先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式的解集
1.3. 数据的收集、整理与描述
1.3.1. 抽样调查:调查部分数据,根据部分来估计总体的调查方式称为抽样调查
1.3.2. 总体∶要考察的全体对象称为总体
1.3.3. 个体∶组成总体的每一个考察对象称为个体
1.3.4. 样本:被抽取的所有个体组成一个样本
1.3.5. 样本容量∶样本中个体的数目称为样本客量
1.3.6. 频数∶一般地,我们称落在不同小组中的数据个数为该组的频数
1.3.7. 组数和组距∶在统计数据时,把数据按照一定的范围分成若干各组,分成组的个数称为组数,每一组两个端点的差叫做组距
1.3.8. 通过调查收集数据的一般步骤
1.3.8.1. 明确周查问题
1.3.8.2. 确定调对象
1.3.8.3. 选择调查方法
1.3.8.4. 展开调查
1.3.8.5. 记录结果
1.3.8.6. 得出结论
1.3.9. 收集数据常用的方法
1.3.9.1. 民意调查∶如投票选举
1.3.9.2. 实地调查∶如现场进行观察、收集、统计数据
1.3.9.3. 媒体调查∶报纸、电视、电话、网络等调查都是媒体调查
1.3.10. 数据的表示方法
1.3.10.1. 统计表∶直观地反映数据的分布规律
1.3.10.2. 折线图∶反映数据的变化趋势
1.3.10.3. 条形图∶反映每个项目的具体数据
1.3.10.4. 扇形图∶反映各部分在总体中所占的百分比
1.3.10.5. 频数分布直方图∶直观形象地反映频数分布情况
1.3.10.6. 频数分布折结图∶在频数分布直方图的基础上,取每一个长方形上边的中点,和左右频数为零与直方图相距半个组距两个点
1.3.11. 调查方式
1.3.11.1. 全面调查,优点是可靠、真实
1.3.11.2. 抽样调查,优点是省时、省力,减少破坏性; 随机抽样调查具有广泛性和代表性
1.3.12. 总体和样本
1.3.12.1. 总体:要考察的所有对象
1.3.12.2. 个体∶组成总体的每一个考察对象
1.3.12.3. 样本:从总体中抽出的所有实际被周查的对象组成一个样本
1.3.13. 画直方图的一般步骤
1.3.13.1. 计算最大值与最小值的差
1.3.13.2. 决定组距与组数,先根据数据个数确定组距,再计算组数
1.3.13.3. 确定分点,并分组
1.3.13.4. 确定分点,并分组
1.3.13.5. 绘制频数分布直方图
1.4. 相交线与平行线
1.4.1. 相交线
1.4.1.1. 两条直线相交所成的四个角中,相邻阳的两个角叫做邻补角,特点是两个角共用一条边,另一条边互为反向延长线,性质是邻补角互补
1.4.1.2. 相排的两个角叫做对顶角,特点是它们的两条边互为反向延长线。性质是对顶角相等
1.4.1.3. ①邻角∶两个角有一茶公共边,它们的另-条边互为反向延长线。具有这种关系的两个角,互为邻角。
1.4.1.4. ②对顶角∶ 两个角有一个公共顶点,并且一个角的两条边,分别是另一个角的两条边的向长线,具有这种关系的两个角,互为对顶角。
1.4.1.5. ③对顶角相等
1.4.2. 垂线
1.4.2.1. 垂直∶如果两条直线相交成直角,那么这两条直互相垂直
1.4.2.2. 垂线∶垂直是相交的一种特殊情形,两条直线垂直,其中一条直线知做另一条直的垂线
1.4.2.3. 垂足∶两条垂交点叫垂足
1.4.2.4. 垂线特点∶过一点有且只有一条直线与已知直线垂直
1.4.2.5. 点到直线的距离∶直线外一点到这条直线的垂线段的长度,叫点到直线的距离
1.4.3. 同位角、内错角、同旁内角
1.4.3.1. 同位角∶(在两条直的同一旁,第三条直同一侧)在两条直线谢上方,又在直线E的同侧,具有这种位置关系的两个角叫同位角。
1.4.3.2. 内错角∶(在两条直线内部,位于第三条直线两侧)在两条直线之间,又在直线的两侧,具有这种位置关系的两个角叫内错角。
1.4.3.3. 同旁内角∶(在两条直线部,位于第三条直线同测)在两条直线之间,又在直线E的同侧,具有这种位置关系的两个角叫同旁内角。
1.4.4. 平行线及其判定
1.4.4.1. 平行线
1.4.4.1.1. 平行∶两条直线不相交。互相平行的两条直线,互为评行线。
1.4.4.1.2. 平行公理∶经过直线外一点,有且只有一条直线与这条直线平行
1.4.4.1.3. 平行公理推论∶平行于同一直绨两条直线互相平行。
1.4.4.2. 平行线的判定
1.4.4.2.1. 两条平行线被第三条直线所截,如果同位角相等,那么这两条直线平行
1.4.4.2.2. 两条平行线被第三条直线所截,如果内错角相,那么这两条直线平行
1.4.4.2.3. 两条平行线被第三条直线所截,如果同降内角互补,那么这两条直线平行
1.4.4.3. 平行线的性质
1.4.4.3.1. 两条平行线被第三条直线所截,同位角相等。(两直线平行,同位角相等)
1.4.4.3.2. 两条平行线被第三条直线所截,同位角相等(两直线平行,内错角相等)
1.4.4.3.3. 两条平行线被第三条直线所截,同降内角互补(两直线平行,同旁内角相等)
1.4.5. 命题、定理、证明
1.4.5.1. 命题的辊况念∶ 判断一件事情骼语句,叫做命题
1.4.5.2. 命题的组成∶每个命题都是题设、结论两部分组成
1.4.5.3. 真命题∶正确的命题,题设成立,结论一定成立
1.4.5.4. 假命题∶ 错误的命题,题设成立,不能保证结论一定成立
1.4.5.5. 定理∶ 经过推理证实得到的真命题。定理可以做为继续推理的依据)
1.4.5.6. 证明∶ 推理的过程叫做证明
1.4.6. 平移
1.4.6.1. 平移∶平移是指在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动加叫做平移
1.4.6.2. 平移的性质
1.4.6.2.1. 把一个图形整体沿某一直线方向移动,会得到一个新图形,新图形与原图形纳形状和大小完全相同
1.4.6.2.2. 新图形冲的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点。连接各组对应点的段平行且相等
1.5. 实数
1.5.1. 平方根
1.5.1.1. 平方根的定义∶如果一个数x的平方等于a,那么这个数x就叫做a的平方根
1.5.1.2. 开平方的定义∶求一个数的平方根的运算,叫做开平方。开平方运算的被开方数必须是非负数才有意义。
1.5.1.3. 平方与开平方互为逆运算
1.5.1.4. 一个正数有两个平方根。即正数进行开平方运算有两个结果
1.5.1.4.1. 一个负数没有平方根,即负数不能进行开平方运算
1.5.1.4.2. 0的平方根是0
1.5.2. 算术平方根
1.5.2.1. 算术平方根的定义∶一般地,如果一个正数x的平方等于a即x²=a,那么这个正数x叫做a的算术平方根
1.5.2.2. 当被开方数扩太时,它的算术平方根也扩大;当被开方数缩小时与它的算术平方根也缩小
1.5.2.3. 正数和零的算术平方根都只有一个,零的算术平方根是零
1.5.3. 立方根
1.5.3.1. 立方根的定义∶如果个数x的立方等于a,这个数叫做a的立方根(也叫做三次方根)
1.5.3.2. 一个正数有一个正的立方根;0有一个立方根,是它本身;一个负数有一个负的立方根;任何数都有唯一的立方根
1.5.3.3. 利用开立方和立方互为逆运算关系,求一个的立方根,就可以利用这种互逆关系,检验其正确性
1.5.3.4. 求负数的立方根,可以先求出这个负数的绝对值的立方根,再取其相反数
1.5.4. 实数的概念及分类
1.5.4.1. 无理数∶像前面的很多数的平方根和立方根都是无限不循环小数,无限不循环小数又叫无理数
1.5.4.2. 实数∶有理数和无理数统称实数
1.5.4.3. 实数的分类
1.5.4.3.1. 整数包括正整数、零、负整数。零和正整数又叫自然数
1.5.4.3.2. 正整数、零、负整数、正分数、负分数统称为有理数
1.5.4.4. 无理数
1.5.4.4.1. 开方开不尽的数
1.5.4.4.2. 有特定意义的数
1.5.4.4.3. 有特定结构的数
1.5.5. 数的倒数、相反数和绝对值
1.5.5.1. 相反数
1.5.5.1.1. 实数与它的相反数是一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零),从数轴上看,互为相反数的两个数所对应的点关于原点对称
1.5.5.2. 绝对值
1.5.5.2.1. 一个数的绝对值就是表示这个数的点与原点的距离
1.5.5.3. 倒数
1.5.5.3.1. 如果a与b互为倒数,则有ab=1,反之亦成立。倒数等于本身的数是1和-1。零没有倒数。
1.5.5.4. 实数与数轴上点的关系
1.5.5.4.1. 每一个无理数都可以用数轴上的一个点表示出来,数轴上的点有些表示有理数,有些表示无理数
1.5.5.4.2. 实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的一个点来表示; 反过来,数轴上的每一个点都是表示一个实数
1.6. 平面直角坐标系
1.6.1. 平面直角坐标系
1.6.1.1. 有序数对
1.6.1.1.1. 1.有序数对∶ 用两个数来表示一个确定的位置,其中两个数自表示不同的意义,我们这种有顺序的两个数组成的数对,叫做有序数对
1.6.1.1.2. 坐标∶数轴或平面上的点可以用一个数或数对)来表示,这个数或数对叫做这个点的坐标
1.6.1.2. 平面直角坐标系
1.6.1.2.1. 平面直角坐标系∶ 在平面内画两条互相垂直,并且有公共原点的数轴
1.6.1.2.2. X轴∶水平的轴叫X 轴或横轴。向右方向为正方向
1.6.1.2.3. Y轴∶ 竖直的轴叫Y 轴或纵轴。向上方向为正方向
1.6.1.2.4. 原点∶两个数轴的交点叫做平面直角坐标系的原点
1.6.1.3. 象限
1.6.1.3.1. 象限∶X轴和Y轴把坐标平面分成四个部分,也叫四个象限。右上面做第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限
1.6.1.3.2. 象限以数轴为界,横轴、纵轴上的点及原点不属于任何象限
1.6.1.3.3. 象限的特点
1.6.1.3.3.1. 特殊位置的点的坐标的特点
1.6.1.3.3.1.1. X轴上的点的纵坐标为零;Y轴上的点的横坐标为零
1.6.1.3.3.1.2. 第一、三象限角平分线上的点横、纵坐标相等,第二、四象限角平分线上的点横、纵坐标互为相反数
1.6.1.3.3.1.3. 在任意的两点中,如果两点的横坐标相同,则两点的连线平行于纵轴;如果两点的纵坐标相同,则两点的连线平行于横轴
1.6.1.3.3.2. 点到轴及原点的距离∶点到x轴的距离为y;点到y轴的距离为x
1.6.2. 坐标方法的简单应用
1.6.2.1. 用坐标表示地理位置的过程
1.6.2.1.1. 建立坐标系,选择一个合适的参照点为原点,确定Ⅹ轴和Y轴的证方向
1.6.2.1.2. 根据具体问题确定适当的比例尺,在坐标轴上标出单位长度
1.6.2.1.3. 在坐标平面内画出这些点,写出各点的坐标和各个地点的名称
1.6.2.2. 用坐标表示平移
1.6.2.2.1. 在平面直角坐标系内,如果把一个图形络个点的横坐标都加或减去一个正数s,平移a个单位长度