如何用思维导图总结小学五年级下册数学知识点?
2021-04-16 18:36:26
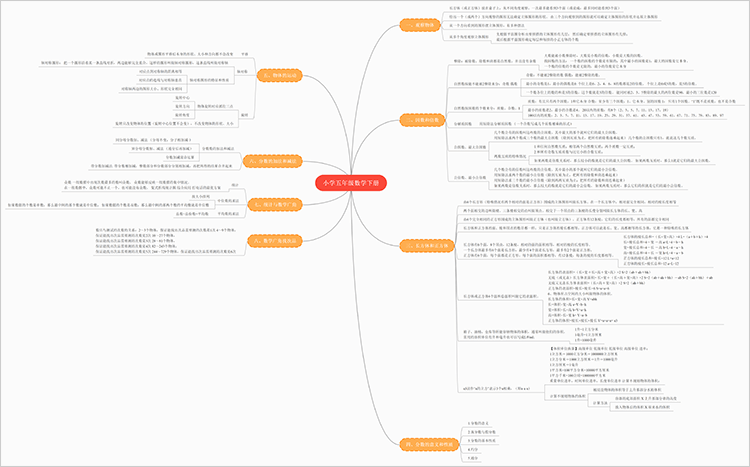
小学五年级下册数学有八个单元,知识点包括观察物体、因数与倍数、长方体与正方体、分数的意义与性质、图形的运动、分数的加法和减法、折线统计图、找次品等。
小学五年级下册数学虽然仅有八个单元,但各单元都有繁多的知识点需要学习。不少同学在学习的过程中,容易出现知识点记忆混乱、理解不清晰或理解错误等问题。为此可以借助思维导图工具,将小学五年级下册数学各单元的知识点总结并归纳至思维导图中,便于整理知识点并体现出其中的重点与重要内容。
1、首先在迅捷画图新建一份思维导图(空白思维导图或套用模板均可)。
注:通常会利用模板库的模板寻找绘制灵感,或节约绘制时间。
2、接着会进入到思维导图编辑页面,此时结合小学五年级下册数学知识点编辑并完善思维导图的内容。
为加快思维导图的制作通常会运用快捷键编辑节点,常用的快捷键有捷键有插入下级节点(Tab)、插入关系线(F4)、插入上级节点(Shift+Tab)、插入同级节点(Enter)、整理布局(Ctrl+Shift+L)。
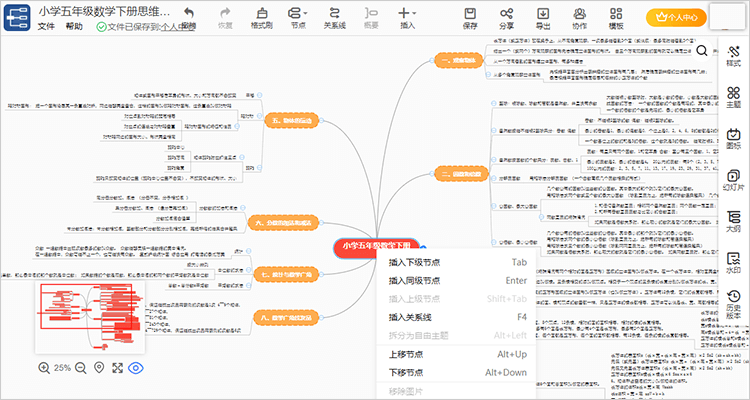
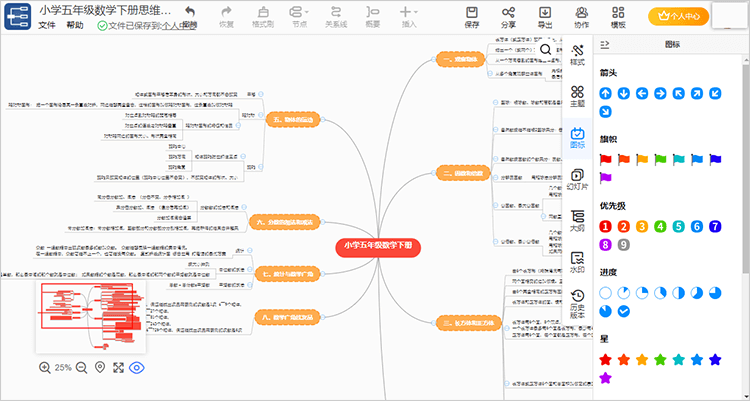
3、编辑过程中看到列表所展现的样式、主题、图标、幻灯片、大纲、水印等功能,可以利用这些功能对思维导图的内容进行美化处理,使之看起来更加美观。
其中要注意的是“图标”功能,总结知识点时可以借助箭头、旗帜、优先级、进度条等类型的符号突出重点与难点内容。
4、当你在没有思路时,也可以利用“协作”功能,邀请协作者和你一同总结归纳知识点。
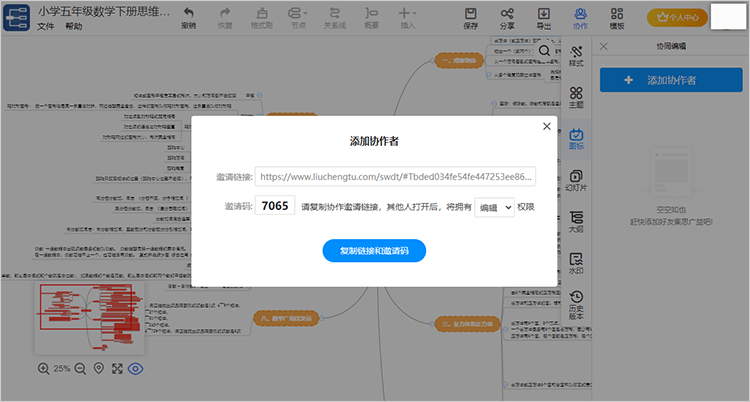
5、小学五年级下册数学知识点总结完毕后,通过“保存”功能将思维导图存储至账号云端,或生成word、ppt、png、pdf等多种格式“导出”至设备本地。
以上就是利用思维导图总结归纳小学五年级下册数学知识点的方法,希望可以帮助到有需要的小伙伴哟!
2、数据云存储:迅捷思维导图支持自动保存制作好的小学五年级下册数学思维导图,并将数据存储到云端,方便更换设备查看。
3、模板丰富:诸多行业的分类模板为制作思维导图提供思路。
4、多人协同:迅捷思维导图支持添加协作者,邀请他人一同绘制小学五年级下册数学思维导图,共同填充内容。
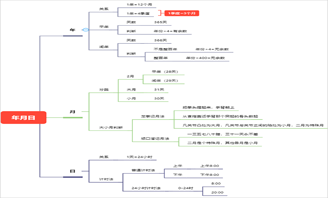
1.1.1. 长方体(或正方体)放在桌子上,从不同角度观察,一次最多能看到3个面(或说成:最多同时能看到3个面)
1.1.2. 给出一个(或两个)方向观察的图形无法确定立体图形的形状。 由三个方向观察到的图形就可以确定立体图形的形状并还原立体图形
1.1.3. 从一个方向看到的图形摆立体图形,有多种摆法
1.1.4. 从多个角度观察立体图形
1.1.4.1. 先根据平面图分析出要拼搭的立体图形有几层; 然后确定要拼搭的立体图形有几排;
最后根据平面图形确定每层和每排的小正方体的个数
1.2. 二、因数和倍数
1.2.1. 整除:被除数、除数和商都是自然数,并且没有余数
1.2.1.1. 大数能被小数整除时,大数是小数的倍数,小数是大数的因数。
找因数的方法: 一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
一个数的倍数的个数是无限的,最小的倍数是它本身
1.2.2. 自然数按能不能被2整除来分:奇数 偶数
1.2.2.1. 奇数:不能被2整除的数 偶数:能被2整除的数。
1.2.2.2. 最小的奇数是1,最小的偶数是0. 个位上是0,2,4,6,8的数都是2的倍数。 个位上是0或5的数,是5的倍数。
1.2.2.3. 一个数各位上的数的和是3的倍数,这个数就是3的倍数。 能同时被2、3、5整除的最大的两位数是90,最小的三位数是120
1.2.3. 自然数按因数的个数来分:质数、合数、1
1.2.3.1. 质数:有且只有两个因数,1和它本身 合数:至少有三个因数,1、它本身、别的因数 1: 只有1个因数。“1”既不是质数,也不是合数
1.2.3.2. 最小的质数是2,最小的合数是4。 20以内的质数:有8个(2、3、5、7、11、13、17、19)
100以内的质数:2、3、5、7、11、13、17、19、23、29、31、37、41、 43、47、53、59、61、67、71、73、79、83、89、97
1.2.4. 分解质因数
1.2.4.1. 用短除法分解质因数 (一个合数写成几个质数相乘的形式)
1.2.5. 公因数、最大公因数
1.2.5.1. 几个数公有的因数叫这些数的公因数。其中最大的那个就叫它们的最大公因数。
用短除法求两个数或三个数的最大公因数 (除到互质为止,把所有的除数连乘起来) 几个数的公因数只有1,就说这几个数互质。
1.2.5.2. 两数互质的特殊情况
1.2.5.2.1. 1.和任何自然数互质;相邻两个自然数互质;两个质数一定互质;
2.和所有奇数互质质数与比它小的合数互质;
1.2.5.2.2. 如果两数是倍数关系时,那么较小的数就是它们的最大公因数。 如果两数互质时,那么1就是它们的最大公因数。
1.2.6. 公倍数、最小公倍数
1.2.6.1. 几个数公有的倍数叫这些数的公倍数。其中最小的那个就叫它们的最小公倍数。
用短除法求两个数的最小公倍数(除到互质为止,把所有的除数和商连乘起来)
用短除法求三个数的最小公倍数(除到两两互质为止,把所有的除数和商连乘起来)
如果两数是倍数关系时,那么较大的数就是它们的最小公倍数。 如果两数互质时,那么它们的积就是它们的最小公倍数。
1.3. 三、长方体和正方体
1.3.1. 由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。在一个长方体中,相对面完全相同,相对的棱长度相等
1.3.2. 两个面相交的边叫做棱。三条棱相交的点叫做顶点。相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高
1.3.3. 由6个完全相同的正方形围成的立体图形叫做正方体(也叫做立方体)。正方体有12条棱,它们的长度都相等,所有的面都完全相同
1.3.4. 长方体和正方体的面、棱和顶点的数目都一样,只是正方体的棱长都相等,正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体
1.3.5. 长方体有6个面,8个顶点,12条棱,相对的面的面积相等,相对的棱的长度相等。
一个长方体最多有6个面是长方形,最少有4个面是长方形,最多有2个面是正方形。
正方体有6个面,每个面都是正方形,每个面的面积都相等,有12条棱,每条的棱的长度都相等。
1.3.5.1. 长方体的棱长总和=(长+宽+高)×4 L=(a+b+h)×4
长=棱长总和÷4-宽 -高 a=L÷4-b-h
宽=棱长总和÷4-长 -高 b=L÷4-a-h
高=棱长总和÷4-长 -宽 h=L÷4-a-b
正方体的棱长总和=棱长×12 L=a×12
正方体的棱长=棱长总和÷12 a=L÷12
1.3.6. 长方体或正方体6个面和总面积叫做它的表面积。
1.3.6.1. 长方体的表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)
无底(或无盖)长方体表面积= 长×宽+(长×高+宽×高)×2 S=2(ab+ah+bh)-ab S=2(ah+bh)+ab
无底又无盖长方体表面积=(长×高+宽×高)×2 S=2(ah+bh)
正方体的表面积=棱长×棱长×6 S=a×a×6
6、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh
长=体积÷宽÷高 a=V÷b÷h
宽=体积÷长÷高 b=V÷a÷h
高=体积÷长÷宽 h= V÷a÷b
正方体的体积=棱长×棱长×棱长 V=a×a×a= a3
1.3.7. 箱子、油桶、仓库等所能容纳物体的体积,通常叫做他们的容积。
常用的容积单位有升和毫升也可以写成L和ml。
1.3.7.1. 1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
1.3.8. a3读作“a的立方”表示3个a相乘,(即a·a·a)
1.3.8.1. 【体积单位换算】高级单位 低级单位 低级单位 高级单位 进率:
1立方米=1000立方分米=1000000立方厘米
1立方分米=1000立方厘米=1升=1000毫升
1立方厘米=1毫升
1平方米=100平方分米=10000平方厘米
1平方千米=100公顷=1000000平方米
重量单位进率,时间单位进率,长度单位进率 计算不规则物体的体积:
1.3.8.2. 计算不规则物体的体积
1.3.8.2.1. 被浸没物体的体积等于上升那部分水的体积
1.3.8.2.2. 计算方法
1.3.8.2.2.1. 容器的底部面积 X 上升那部分谁的高度
1.3.8.2.2.2. 放入物体后的体积 X 原来水的体积
1.4. 四、分数的意义和性质
1.4.1. 1.分数的意义
1.4.2. 2.真分数与假分数
1.4.3. 3.分数的基本性质
1.4.4. 4.约分
1.4.5. 5.通分
1.5. 五、物体的运动
1.5.1. 平移
1.5.1.1. 物体或图形平移后本身的形状、大小和方向都不会改变
1.5.2. 轴对称
1.5.2.1. 轴对称图形: 把一个图形沿着某一条直线对折,两边能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴
1.5.2.2. 轴对称图形的特征和性质
1.5.2.2.1. 对应点到对称轴的距离相等
1.5.2.2.2. 对应点的连线与对称轴垂直
1.5.2.2.3. 对称轴两边的图形大小、形状完全相同
1.5.3. 旋转
1.5.3.1. 物体旋转时应抓住三点
1.5.3.1.1. 旋转中心
1.5.3.1.2. 旋转方向
1.5.3.1.3. 旋转角度
1.5.3.2. 旋转只改变物体的位置(旋转中心位置不会变),不改变物体的形状、大小
1.6. 六、分数的加法和减法
1.6.1. 分数数的加法和减法
1.6.1.1. 同分母分数加、减法 (分母不变,分子相加减 )
1.6.1.2. 异分母分数加、减法 (通分后再加减)
1.6.1.3. 分数加减混合运算
1.6.2. 带分数加减法: 带分数相加减,整数部分和分数部分分别相加减,再把所得的结果合并起来
1.7. 七、统计与数学广角
1.7.1. 统计
1.7.1.1. 众数 一组数据中出现次数最多的数叫众数。 众数能够反映一组数据的集中情况。
在一组数据中,众数可能不止一个,也可能没有众数。 复式折线统计图 综合应用 打电话的最优方案
1.7.2. 中位数的求法
1.7.2.1. 按大小排列
1.7.2.2. 如果数据的个数是单数,那么最中间的那个数就是中位数; 如果数据的个数是双数,那么最中间的那两个数的平均数就是中位数
1.7.3. 平均数的求法
1.7.3.1. 总数÷总份数=平均数
1.8. 八、数学广角找次品
1.8.1. 数目与测试的次数的关系:2~3个物体,保证能找出次品需要测的次数是1次 4~9个物体,
保证能找出次品需要测的次数是2次 10~27个物体,
保证能找出次品需要测的次数是3次 28~81个物体,
保证能找出次品需要测的次数是4次 82~243个物体,
保证能找出次品需要测的次数是5次 244~729个物体,保证能找出次品需要测的次数是6次
小学五年级下册数学虽然仅有八个单元,但各单元都有繁多的知识点需要学习。不少同学在学习的过程中,容易出现知识点记忆混乱、理解不清晰或理解错误等问题。为此可以借助思维导图工具,将小学五年级下册数学各单元的知识点总结并归纳至思维导图中,便于整理知识点并体现出其中的重点与重要内容。

思维导图软件
迅捷画图是一款操作简单且好用的思维导图绘制工具,可以帮我们简单绘制小学五年级下册数学思维导图,总结知识点。软件除了日常需要使用到的添加、删除、拖拽节点外,支持给节点添加格式与GFM语法书写的备注帮助我们整理知识点,同时还支持使用“协作”功能邀请他人一同将知识点总结并归纳至思维导图中。如何绘制小学五年级下册数学思维导图
绘制小学五年级下册数学思维导图总结知识点的方法并不难,结合思维导图简单画法从中心主题开始延伸内容,利用思维导图上下层级隶属关系总结知识点即可。1、首先在迅捷画图新建一份思维导图(空白思维导图或套用模板均可)。
注:通常会利用模板库的模板寻找绘制灵感,或节约绘制时间。

2、接着会进入到思维导图编辑页面,此时结合小学五年级下册数学知识点编辑并完善思维导图的内容。
为加快思维导图的制作通常会运用快捷键编辑节点,常用的快捷键有捷键有插入下级节点(Tab)、插入关系线(F4)、插入上级节点(Shift+Tab)、插入同级节点(Enter)、整理布局(Ctrl+Shift+L)。

3、编辑过程中看到列表所展现的样式、主题、图标、幻灯片、大纲、水印等功能,可以利用这些功能对思维导图的内容进行美化处理,使之看起来更加美观。
其中要注意的是“图标”功能,总结知识点时可以借助箭头、旗帜、优先级、进度条等类型的符号突出重点与难点内容。

4、当你在没有思路时,也可以利用“协作”功能,邀请协作者和你一同总结归纳知识点。

5、小学五年级下册数学知识点总结完毕后,通过“保存”功能将思维导图存储至账号云端,或生成word、ppt、png、pdf等多种格式“导出”至设备本地。

以上就是利用思维导图总结归纳小学五年级下册数学知识点的方法,希望可以帮助到有需要的小伙伴哟!
为什么要用迅捷画图制作小学五年级下册数学思维导图?
1、多平台制作:迅捷思维导图支持在线和软件制作,其中在线制图方式可在Windows、mac等设备的浏览器中使用。2、数据云存储:迅捷思维导图支持自动保存制作好的小学五年级下册数学思维导图,并将数据存储到云端,方便更换设备查看。
3、模板丰富:诸多行业的分类模板为制作思维导图提供思路。
4、多人协同:迅捷思维导图支持添加协作者,邀请他人一同绘制小学五年级下册数学思维导图,共同填充内容。
小学五年级下册数学思维导图大纲
1.1. 一、观察物体1.1.1. 长方体(或正方体)放在桌子上,从不同角度观察,一次最多能看到3个面(或说成:最多同时能看到3个面)
1.1.2. 给出一个(或两个)方向观察的图形无法确定立体图形的形状。 由三个方向观察到的图形就可以确定立体图形的形状并还原立体图形
1.1.3. 从一个方向看到的图形摆立体图形,有多种摆法
1.1.4. 从多个角度观察立体图形
1.1.4.1. 先根据平面图分析出要拼搭的立体图形有几层; 然后确定要拼搭的立体图形有几排;
最后根据平面图形确定每层和每排的小正方体的个数
1.2. 二、因数和倍数
1.2.1. 整除:被除数、除数和商都是自然数,并且没有余数
1.2.1.1. 大数能被小数整除时,大数是小数的倍数,小数是大数的因数。
找因数的方法: 一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
一个数的倍数的个数是无限的,最小的倍数是它本身
1.2.2. 自然数按能不能被2整除来分:奇数 偶数
1.2.2.1. 奇数:不能被2整除的数 偶数:能被2整除的数。
1.2.2.2. 最小的奇数是1,最小的偶数是0. 个位上是0,2,4,6,8的数都是2的倍数。 个位上是0或5的数,是5的倍数。
1.2.2.3. 一个数各位上的数的和是3的倍数,这个数就是3的倍数。 能同时被2、3、5整除的最大的两位数是90,最小的三位数是120
1.2.3. 自然数按因数的个数来分:质数、合数、1
1.2.3.1. 质数:有且只有两个因数,1和它本身 合数:至少有三个因数,1、它本身、别的因数 1: 只有1个因数。“1”既不是质数,也不是合数
1.2.3.2. 最小的质数是2,最小的合数是4。 20以内的质数:有8个(2、3、5、7、11、13、17、19)
100以内的质数:2、3、5、7、11、13、17、19、23、29、31、37、41、 43、47、53、59、61、67、71、73、79、83、89、97
1.2.4. 分解质因数
1.2.4.1. 用短除法分解质因数 (一个合数写成几个质数相乘的形式)
1.2.5. 公因数、最大公因数
1.2.5.1. 几个数公有的因数叫这些数的公因数。其中最大的那个就叫它们的最大公因数。
用短除法求两个数或三个数的最大公因数 (除到互质为止,把所有的除数连乘起来) 几个数的公因数只有1,就说这几个数互质。
1.2.5.2. 两数互质的特殊情况
1.2.5.2.1. 1.和任何自然数互质;相邻两个自然数互质;两个质数一定互质;
2.和所有奇数互质质数与比它小的合数互质;
1.2.5.2.2. 如果两数是倍数关系时,那么较小的数就是它们的最大公因数。 如果两数互质时,那么1就是它们的最大公因数。
1.2.6. 公倍数、最小公倍数
1.2.6.1. 几个数公有的倍数叫这些数的公倍数。其中最小的那个就叫它们的最小公倍数。
用短除法求两个数的最小公倍数(除到互质为止,把所有的除数和商连乘起来)
用短除法求三个数的最小公倍数(除到两两互质为止,把所有的除数和商连乘起来)
如果两数是倍数关系时,那么较大的数就是它们的最小公倍数。 如果两数互质时,那么它们的积就是它们的最小公倍数。
1.3. 三、长方体和正方体
1.3.1. 由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。在一个长方体中,相对面完全相同,相对的棱长度相等
1.3.2. 两个面相交的边叫做棱。三条棱相交的点叫做顶点。相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高
1.3.3. 由6个完全相同的正方形围成的立体图形叫做正方体(也叫做立方体)。正方体有12条棱,它们的长度都相等,所有的面都完全相同
1.3.4. 长方体和正方体的面、棱和顶点的数目都一样,只是正方体的棱长都相等,正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体
1.3.5. 长方体有6个面,8个顶点,12条棱,相对的面的面积相等,相对的棱的长度相等。
一个长方体最多有6个面是长方形,最少有4个面是长方形,最多有2个面是正方形。
正方体有6个面,每个面都是正方形,每个面的面积都相等,有12条棱,每条的棱的长度都相等。
1.3.5.1. 长方体的棱长总和=(长+宽+高)×4 L=(a+b+h)×4
长=棱长总和÷4-宽 -高 a=L÷4-b-h
宽=棱长总和÷4-长 -高 b=L÷4-a-h
高=棱长总和÷4-长 -宽 h=L÷4-a-b
正方体的棱长总和=棱长×12 L=a×12
正方体的棱长=棱长总和÷12 a=L÷12
1.3.6. 长方体或正方体6个面和总面积叫做它的表面积。
1.3.6.1. 长方体的表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)
无底(或无盖)长方体表面积= 长×宽+(长×高+宽×高)×2 S=2(ab+ah+bh)-ab S=2(ah+bh)+ab
无底又无盖长方体表面积=(长×高+宽×高)×2 S=2(ah+bh)
正方体的表面积=棱长×棱长×6 S=a×a×6
6、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh
长=体积÷宽÷高 a=V÷b÷h
宽=体积÷长÷高 b=V÷a÷h
高=体积÷长÷宽 h= V÷a÷b
正方体的体积=棱长×棱长×棱长 V=a×a×a= a3
1.3.7. 箱子、油桶、仓库等所能容纳物体的体积,通常叫做他们的容积。
常用的容积单位有升和毫升也可以写成L和ml。
1.3.7.1. 1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
1.3.8. a3读作“a的立方”表示3个a相乘,(即a·a·a)
1.3.8.1. 【体积单位换算】高级单位 低级单位 低级单位 高级单位 进率:
1立方米=1000立方分米=1000000立方厘米
1立方分米=1000立方厘米=1升=1000毫升
1立方厘米=1毫升
1平方米=100平方分米=10000平方厘米
1平方千米=100公顷=1000000平方米
重量单位进率,时间单位进率,长度单位进率 计算不规则物体的体积:
1.3.8.2. 计算不规则物体的体积
1.3.8.2.1. 被浸没物体的体积等于上升那部分水的体积
1.3.8.2.2. 计算方法
1.3.8.2.2.1. 容器的底部面积 X 上升那部分谁的高度
1.3.8.2.2.2. 放入物体后的体积 X 原来水的体积
1.4. 四、分数的意义和性质
1.4.1. 1.分数的意义
1.4.2. 2.真分数与假分数
1.4.3. 3.分数的基本性质
1.4.4. 4.约分
1.4.5. 5.通分
1.5. 五、物体的运动
1.5.1. 平移
1.5.1.1. 物体或图形平移后本身的形状、大小和方向都不会改变
1.5.2. 轴对称
1.5.2.1. 轴对称图形: 把一个图形沿着某一条直线对折,两边能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴
1.5.2.2. 轴对称图形的特征和性质
1.5.2.2.1. 对应点到对称轴的距离相等
1.5.2.2.2. 对应点的连线与对称轴垂直
1.5.2.2.3. 对称轴两边的图形大小、形状完全相同
1.5.3. 旋转
1.5.3.1. 物体旋转时应抓住三点
1.5.3.1.1. 旋转中心
1.5.3.1.2. 旋转方向
1.5.3.1.3. 旋转角度
1.5.3.2. 旋转只改变物体的位置(旋转中心位置不会变),不改变物体的形状、大小
1.6. 六、分数的加法和减法
1.6.1. 分数数的加法和减法
1.6.1.1. 同分母分数加、减法 (分母不变,分子相加减 )
1.6.1.2. 异分母分数加、减法 (通分后再加减)
1.6.1.3. 分数加减混合运算
1.6.2. 带分数加减法: 带分数相加减,整数部分和分数部分分别相加减,再把所得的结果合并起来
1.7. 七、统计与数学广角
1.7.1. 统计
1.7.1.1. 众数 一组数据中出现次数最多的数叫众数。 众数能够反映一组数据的集中情况。
在一组数据中,众数可能不止一个,也可能没有众数。 复式折线统计图 综合应用 打电话的最优方案
1.7.2. 中位数的求法
1.7.2.1. 按大小排列
1.7.2.2. 如果数据的个数是单数,那么最中间的那个数就是中位数; 如果数据的个数是双数,那么最中间的那两个数的平均数就是中位数
1.7.3. 平均数的求法
1.7.3.1. 总数÷总份数=平均数
1.8. 八、数学广角找次品
1.8.1. 数目与测试的次数的关系:2~3个物体,保证能找出次品需要测的次数是1次 4~9个物体,
保证能找出次品需要测的次数是2次 10~27个物体,
保证能找出次品需要测的次数是3次 28~81个物体,
保证能找出次品需要测的次数是4次 82~243个物体,
保证能找出次品需要测的次数是5次 244~729个物体,保证能找出次品需要测的次数是6次