有理数思维导图整理,简单归纳知识点
2023-06-05 16:08:23
有理数是整数和分数的统称,也是整数和分数的集合,在人教版七年级上册数学第一章就会学习到,涉及有整数和负数及有理数的概念、分类、运算、比较大小与运算定律等内容。
在以往,多数同学会以摘抄的形式梳理知识内容,本节迅哥给大家分享有理数思维导图,利用思维导图工具以层层递进的方式由浅至深系统地整理有理数内容,一起来看看吧~~
接着围绕有理数的各部分内容继续进一步归纳相关知识内容:
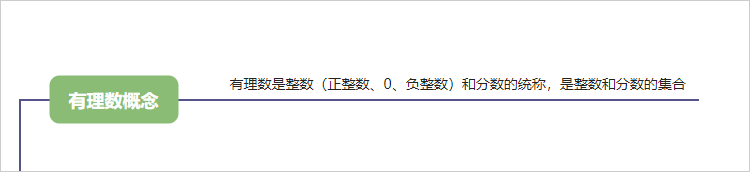
1、有理数概念
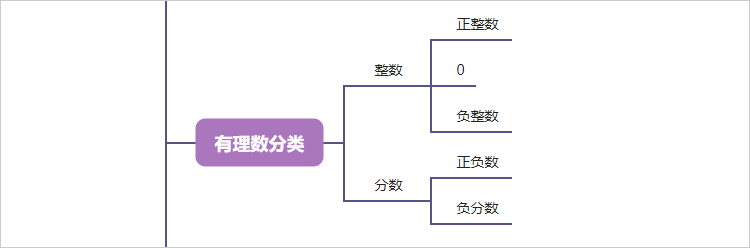
2、有理数分类
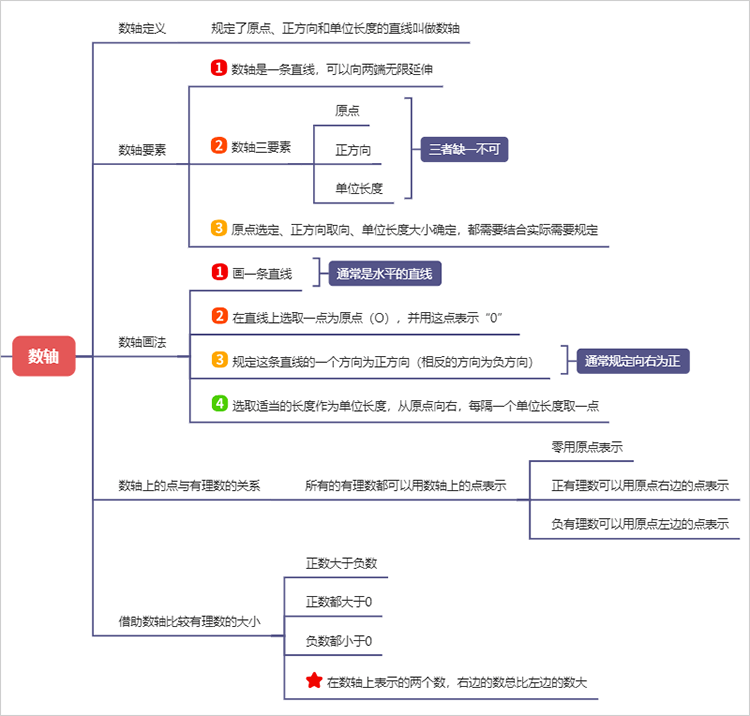
3、数轴
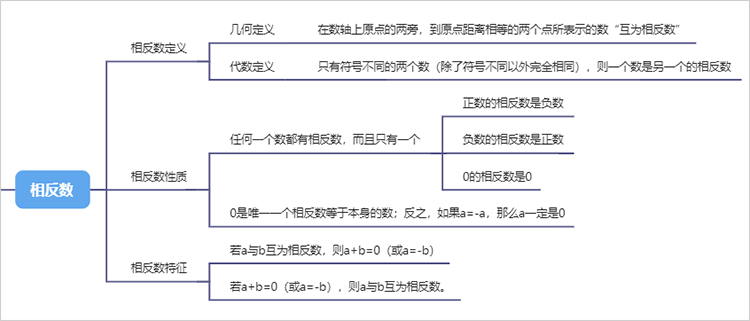
4、相反数
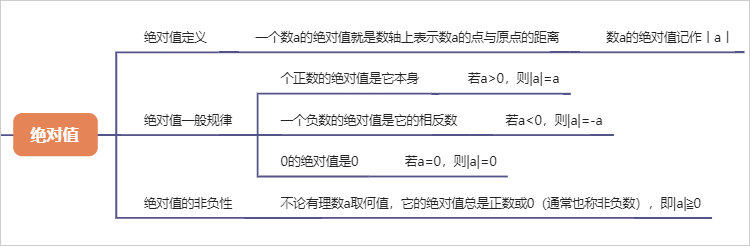
5、绝对值
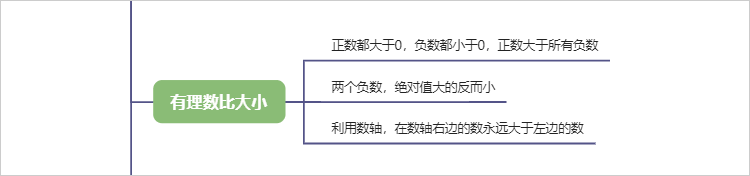
6、有理数比大小
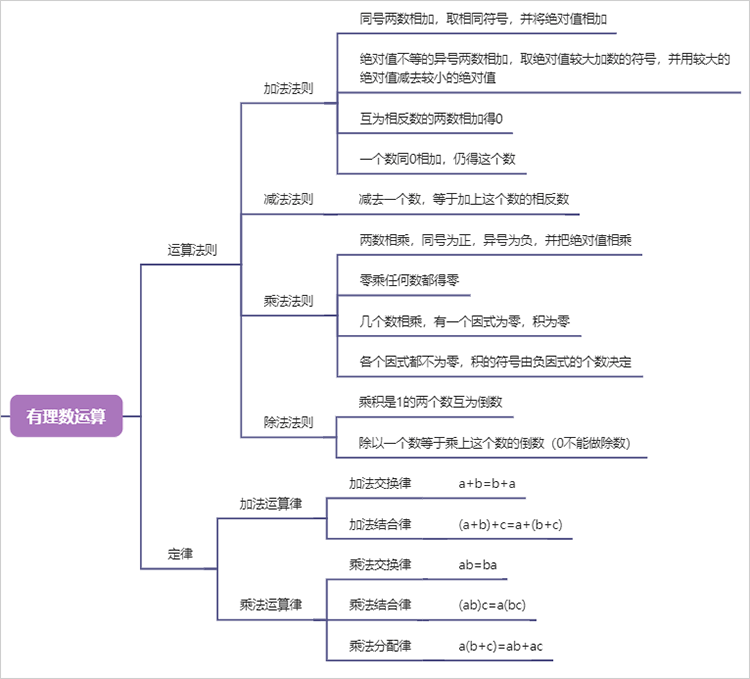
7、有理数运算
由于有理数的知识内容较多,在梳理内容时,还可以试着用工具栏的“大纲”功能以笔记大纲的风格梳理内容。
以上就是本期关于有理数思维导图的内容啦,数学作为一门重要的学科,涉及到各领域,若没有一定的学习技巧可能难以将其中的逻辑化为己有,可以试着用思维导图梳理知识内容,辅助学习哟!
1.1. 有理数概念
1.1.1. 有理数是整数(正整数、0、负整数)和分数的统称,是整数和分数的集合
1.2. 有理数分类
1.2.1. 整数
1.2.1.1. 正整数
1.2.1.2. 0
1.2.1.3. 负整数
1.2.2. 分数
1.2.2.1. 正负数
1.2.2.2. 负分数
1.3. 数轴
1.3.1. 数轴定义
1.3.1.1. 规定了原点、正方向和单位长度的直线叫做数轴
1.3.2. 数轴要素
1.3.2.1. 数轴是一条直线,可以向两端无限延伸
1.3.2.2. 数轴三要素
1.3.2.2.1. 原点
1.3.2.2.2. 正方向
1.3.2.2.3. 单位长度
1.3.2.3. 原点选定、正方向取向、单位长度大小确定,都需要结合实际需要规定
1.3.3. 数轴画法
1.3.3.1. 画一条直线
1.3.3.2. 在直线上选取一点为原点(O),并用这点表示“0”
1.3.3.3. 规定这条直线的一个方向为正方向(相反的方向为负方向)
1.3.3.4. 选取适当的长度作为单位长度,从原点向右,每隔一个单位长度取一点
1.3.4. 数轴上的点与有理数的关系
1.3.4.1. 所有的有理数都可以用数轴上的点表示
1.3.4.1.1. 零用原点表示
1.3.4.1.2. 正有理数可以用原点右边的点表示
1.3.4.1.3. 负有理数可以用原点左边的点表示
1.3.5. 借助数轴比较有理数的大小
1.3.5.1. 正数大于负数
1.3.5.2. 正数都大于0
1.3.5.3. 负数都小于0
1.3.5.4. 在数轴上表示的两个数,右边的数总比左边的数大
1.4. 相反数
1.4.1. 相反数定义
1.4.1.1. 几何定义
1.4.1.1.1. 在数轴上原点的两旁,到原点距离相等的两个点所表示的数“互为相反数”
1.4.1.2. 代数定义
1.4.1.2.1. 只有符号不同的两个数(除了符号不同以外完全相同),则一个数是另一个的相反数
1.4.2. 相反数性质
1.4.2.1. 任何一个数都有相反数,而且只有一个
1.4.2.1.1. 正数的相反数是负数
1.4.2.1.2. 负数的相反数是正数
1.4.2.1.3. 0的相反数是0
1.4.2.2. 0是唯一一个相反数等于本身的数;反之,如果a=-a,那么a一定是0
1.4.3. 相反数特征
1.4.3.1. 若a与b互为相反数,则a+b=0(或a=-b)
1.4.3.2. 若a+b=0(或a=-b),则a与b互为相反数。
1.5. 绝对值
1.5.1. 绝对值定义
1.5.1.1. 一个数a的绝对值就是数轴上表示数a的点与原点的距离
1.5.1.1.1. 数a的绝对值记作丨a丨
1.5.2. 绝对值一般规律
1.5.2.1. 个正数的绝对值是它本身
1.5.2.1.1. 若a>0,则|a|=a
1.5.2.2. 一个负数的绝对值是它的相反数
1.5.2.2.1. 若a<0,则|a|=-a
1.5.2.3. 0的绝对值是0
1.5.2.3.1. 若a=0,则|a|=0
1.5.3. 绝对值的非负性
1.5.3.1. 不论有理数a取何值,它的绝对值总是正数或0(通常也称非负数),即|a|≧0
1.6. 有理数比大小
1.6.1. 正数都大于0,负数都小于0,正数大于所有负数
1.6.2. 两个负数,绝对值大的反而小
1.6.3. 利用数轴,在数轴右边的数永远大于左边的数
1.7. 有理数运算
1.7.1. 运算法则
1.7.1.1. 加法法则
1.7.1.1.1. 同号两数相加,取相同符号,并将绝对值相加
1.7.1.1.2. 绝对值不等的异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值
1.7.1.1.3. 互为相反数的两数相加得0
1.7.1.1.4. 一个数同0相加,仍得这个数
1.7.1.2. 减法法则
1.7.1.2.1. 减去一个数,等于加上这个数的相反数
1.7.1.3. 乘法法则
1.7.1.3.1. 两数相乘,同号为正,异号为负,并把绝对值相乘
1.7.1.3.2. 零乘任何数都得零
1.7.1.3.3. 几个数相乘,有一个因式为零,积为零
1.7.1.3.4. 各个因式都不为零,积的符号由负因式的个数决定
1.7.1.4. 除法法则
1.7.1.4.1. 乘积是1的两个数互为倒数
1.7.1.4.2. 除以一个数等于乘上这个数的倒数(0不能做除数)
1.7.2. 定律
1.7.2.1. 加法运算律
1.7.2.1.1. 加法交换律
1.7.2.1.1.1. a+b=b+a
1.7.2.1.2. 加法结合律
1.7.2.1.2.1. (a+b)+c=a+(b+c)
1.7.2.2. 乘法运算律
1.7.2.2.1. 乘法交换律
1.7.2.2.1.1. ab=ba
1.7.2.2.2. 乘法结合律
1.7.2.2.2.1. (ab)c=a(bc)
1.7.2.2.3. 乘法分配律
1.7.2.2.3.1. a(b+c)=ab+ac
在以往,多数同学会以摘抄的形式梳理知识内容,本节迅哥给大家分享有理数思维导图,利用思维导图工具以层层递进的方式由浅至深系统地整理有理数内容,一起来看看吧~~

一、有理数思维导图
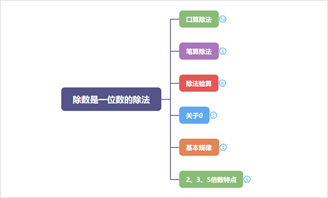
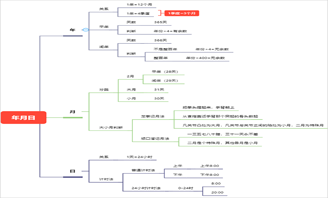
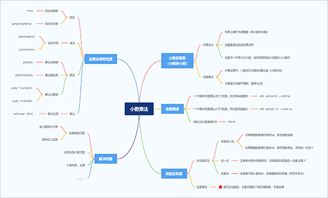
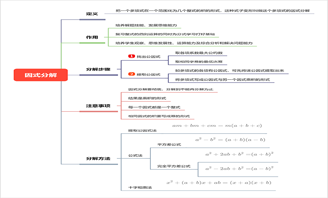
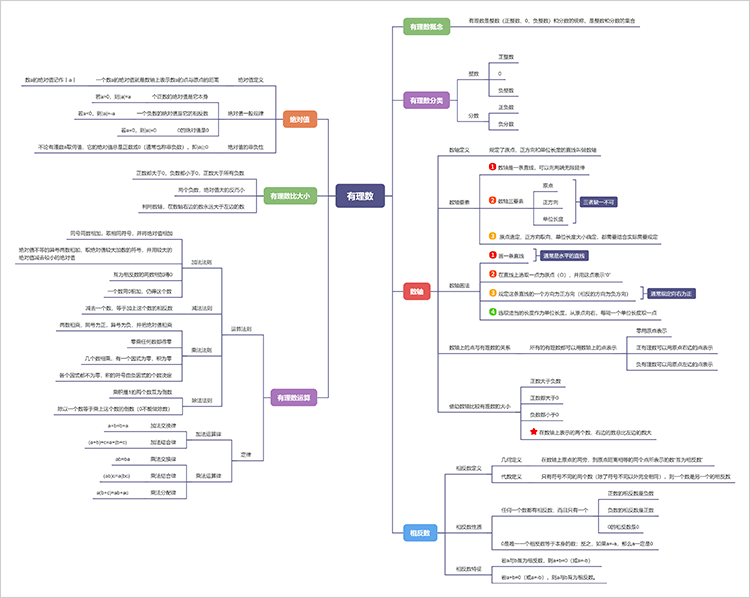
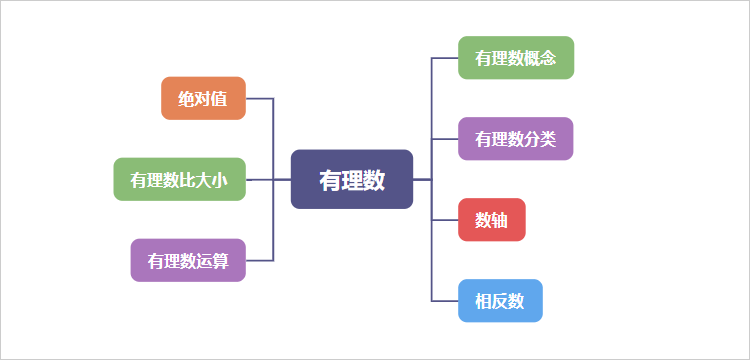
可以看到,该张思维导图对有理数的内容进行了简单梳理,以“七年级上册数学有理数”为主题梳理了与之相关的有理数概念、有理数分类、数轴、相反数、绝对值、有理数比大小、有理数运算七部分。
接着围绕有理数的各部分内容继续进一步归纳相关知识内容:
1、有理数概念

2、有理数分类

3、数轴

4、相反数

5、绝对值

6、有理数比大小

7、有理数运算

由于有理数的知识内容较多,在梳理内容时,还可以试着用工具栏的“大纲”功能以笔记大纲的风格梳理内容。

以上就是本期关于有理数思维导图的内容啦,数学作为一门重要的学科,涉及到各领域,若没有一定的学习技巧可能难以将其中的逻辑化为己有,可以试着用思维导图梳理知识内容,辅助学习哟!
二、《有理数思维导图》大纲
1. 有理数1.1. 有理数概念
1.1.1. 有理数是整数(正整数、0、负整数)和分数的统称,是整数和分数的集合
1.2. 有理数分类
1.2.1. 整数
1.2.1.1. 正整数
1.2.1.2. 0
1.2.1.3. 负整数
1.2.2. 分数
1.2.2.1. 正负数
1.2.2.2. 负分数
1.3. 数轴
1.3.1. 数轴定义
1.3.1.1. 规定了原点、正方向和单位长度的直线叫做数轴
1.3.2. 数轴要素
1.3.2.1. 数轴是一条直线,可以向两端无限延伸
1.3.2.2. 数轴三要素
1.3.2.2.1. 原点
1.3.2.2.2. 正方向
1.3.2.2.3. 单位长度
1.3.2.3. 原点选定、正方向取向、单位长度大小确定,都需要结合实际需要规定
1.3.3. 数轴画法
1.3.3.1. 画一条直线
1.3.3.2. 在直线上选取一点为原点(O),并用这点表示“0”
1.3.3.3. 规定这条直线的一个方向为正方向(相反的方向为负方向)
1.3.3.4. 选取适当的长度作为单位长度,从原点向右,每隔一个单位长度取一点
1.3.4. 数轴上的点与有理数的关系
1.3.4.1. 所有的有理数都可以用数轴上的点表示
1.3.4.1.1. 零用原点表示
1.3.4.1.2. 正有理数可以用原点右边的点表示
1.3.4.1.3. 负有理数可以用原点左边的点表示
1.3.5. 借助数轴比较有理数的大小
1.3.5.1. 正数大于负数
1.3.5.2. 正数都大于0
1.3.5.3. 负数都小于0
1.3.5.4. 在数轴上表示的两个数,右边的数总比左边的数大
1.4. 相反数
1.4.1. 相反数定义
1.4.1.1. 几何定义
1.4.1.1.1. 在数轴上原点的两旁,到原点距离相等的两个点所表示的数“互为相反数”
1.4.1.2. 代数定义
1.4.1.2.1. 只有符号不同的两个数(除了符号不同以外完全相同),则一个数是另一个的相反数
1.4.2. 相反数性质
1.4.2.1. 任何一个数都有相反数,而且只有一个
1.4.2.1.1. 正数的相反数是负数
1.4.2.1.2. 负数的相反数是正数
1.4.2.1.3. 0的相反数是0
1.4.2.2. 0是唯一一个相反数等于本身的数;反之,如果a=-a,那么a一定是0
1.4.3. 相反数特征
1.4.3.1. 若a与b互为相反数,则a+b=0(或a=-b)
1.4.3.2. 若a+b=0(或a=-b),则a与b互为相反数。
1.5. 绝对值
1.5.1. 绝对值定义
1.5.1.1. 一个数a的绝对值就是数轴上表示数a的点与原点的距离
1.5.1.1.1. 数a的绝对值记作丨a丨
1.5.2. 绝对值一般规律
1.5.2.1. 个正数的绝对值是它本身
1.5.2.1.1. 若a>0,则|a|=a
1.5.2.2. 一个负数的绝对值是它的相反数
1.5.2.2.1. 若a<0,则|a|=-a
1.5.2.3. 0的绝对值是0
1.5.2.3.1. 若a=0,则|a|=0
1.5.3. 绝对值的非负性
1.5.3.1. 不论有理数a取何值,它的绝对值总是正数或0(通常也称非负数),即|a|≧0
1.6. 有理数比大小
1.6.1. 正数都大于0,负数都小于0,正数大于所有负数
1.6.2. 两个负数,绝对值大的反而小
1.6.3. 利用数轴,在数轴右边的数永远大于左边的数
1.7. 有理数运算
1.7.1. 运算法则
1.7.1.1. 加法法则
1.7.1.1.1. 同号两数相加,取相同符号,并将绝对值相加
1.7.1.1.2. 绝对值不等的异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值
1.7.1.1.3. 互为相反数的两数相加得0
1.7.1.1.4. 一个数同0相加,仍得这个数
1.7.1.2. 减法法则
1.7.1.2.1. 减去一个数,等于加上这个数的相反数
1.7.1.3. 乘法法则
1.7.1.3.1. 两数相乘,同号为正,异号为负,并把绝对值相乘
1.7.1.3.2. 零乘任何数都得零
1.7.1.3.3. 几个数相乘,有一个因式为零,积为零
1.7.1.3.4. 各个因式都不为零,积的符号由负因式的个数决定
1.7.1.4. 除法法则
1.7.1.4.1. 乘积是1的两个数互为倒数
1.7.1.4.2. 除以一个数等于乘上这个数的倒数(0不能做除数)
1.7.2. 定律
1.7.2.1. 加法运算律
1.7.2.1.1. 加法交换律
1.7.2.1.1.1. a+b=b+a
1.7.2.1.2. 加法结合律
1.7.2.1.2.1. (a+b)+c=a+(b+c)
1.7.2.2. 乘法运算律
1.7.2.2.1. 乘法交换律
1.7.2.2.1.1. ab=ba
1.7.2.2.2. 乘法结合律
1.7.2.2.2.1. (ab)c=a(bc)
1.7.2.2.3. 乘法分配律
1.7.2.2.3.1. a(b+c)=ab+ac