混合运算的思维导图整理
2023-07-27 13:43:52
小学所学的混合运算包括加、减、乘、除四种基本运算,以及加减乘除的混合运算。混合运算是小学数学的基础与重点,下面给大家分享混合运算的思维导图,方便大家用思维导图工具整理混合运算的知识内容。
1、清晰的结构化:通过思维导图的节点和分支,可以清晰地显示混合运算中各个元素之间的关系和层级结构。
2、提升思维的连贯性:通过思维导图的分支和连接,可以帮助你将混合运算中的不同要素进行组织和关联。有助于你更好地理解不同要素之间的逻辑关系,促进思维的连贯性和逻辑性。
3、复习和梳理知识:思维导图可用于有序地梳理知识,通过绘制混合运算的思维导图,你可以整理和总结相关知识点,加深对混合运算概念的理解。
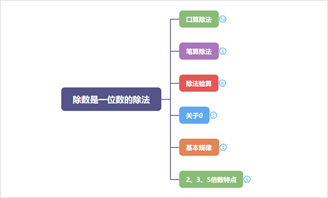
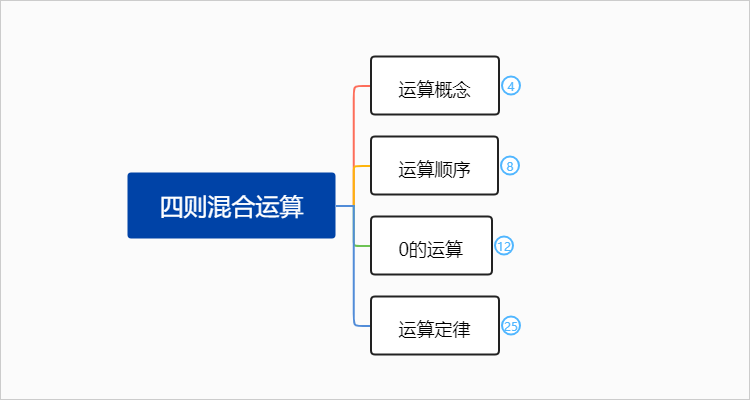
1、运算概念
2、运算顺序
3、0的运算
4、运算定律

1、首先进入到迅捷思维导图的编辑页面;
2、接着将需要梳理的内容呈现至编辑器的中心节点内,即:混合运算;
3、随后以层层递进的方式有序将混合运算相关知识内容填充至分支节点;
4、后续还可以通过插入图标、图片、备注或修改主题、样式等方式进一步完善混合运算的思维导图;
5、当混合运算的思维导图绘制完毕后,将图示存储为png、pdf、json等格式即可。
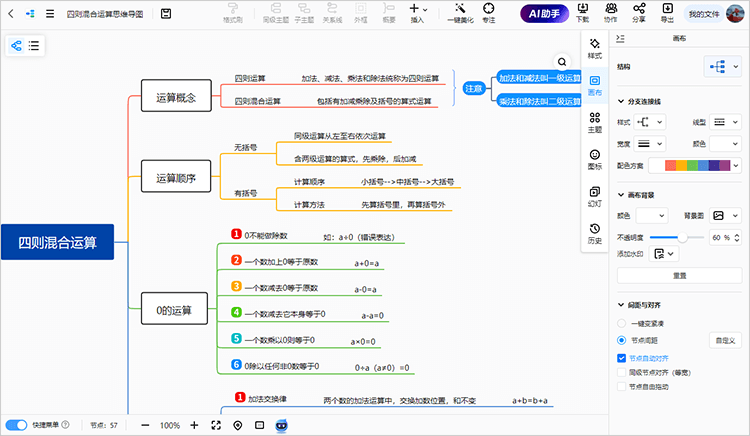
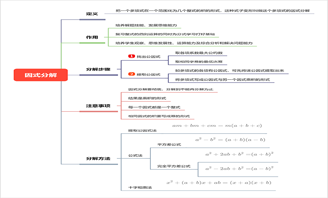
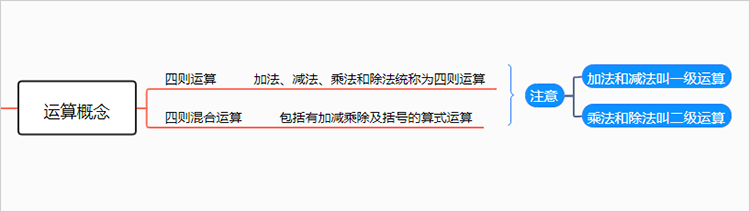
1.1.1. 四则运算
1.1.1.1. 加法、减法、乘法和除法统称为四则运算
1.1.2. 四则混合运算
1.1.2.1. 包括有加减乘除及括号的算式运算
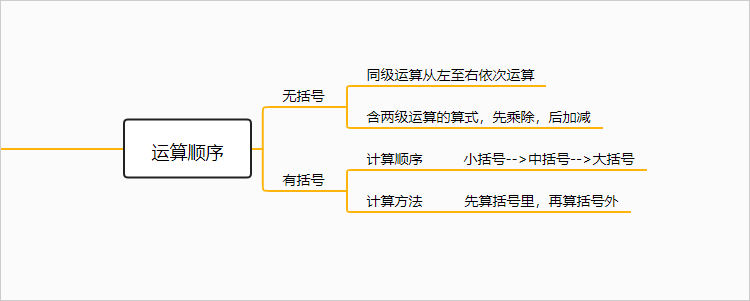
1.2. 运算顺序
1.2.1. 无括号
1.2.1.1. 同级运算从左至右依次运算
1.2.1.2. 含两级运算的算式,先乘除,后加减
1.2.2. 有括号
1.2.2.1. 计算顺序
1.2.2.1.1. 小括号-->中括号-->大括号
1.2.2.2. 计算方法
1.2.2.2.1. 先算括号里,再算括号外
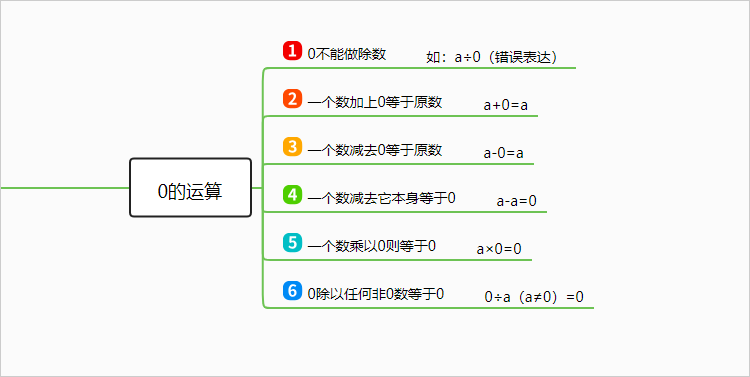
1.3. 0的运算
1.3.1. 0不能做除数
1.3.1.1. 如:a÷0(错误表达)
1.3.2. 一个数加上0等于原数
1.3.2.1. a+0=a
1.3.3. 一个数减去0等于原数
1.3.3.1. a-0=a
1.3.4. 一个数减去它本身等于0
1.3.4.1. a-a=0
1.3.5. 一个数乘以0则等于0
1.3.5.1. a×0=0
1.3.6. 0除以任何非0数等于0
1.3.6.1. 0÷a(a≠0)=0
1.4. 运算定律
1.4.1. 加法交换律
1.4.1.1. 两个数的加法运算中,交换加数位置,和不变
1.4.1.1.1. a+b=b+a
1.4.2. 加法结合律
1.4.2.1. 三个数相加,先把前两个数相加,或者先把后两个数相加,和不变
1.4.2.1.1. (a+b)+c=a+(b+c)
1.4.3. 乘法交换律
1.4.3.1. 两个数相乘的乘法运算中,交换两乘数位置,积不变
1.4.3.1.1. a×b=b×a
1.4.4. 乘法结合律
1.4.4.1. 三个数相乘,先把前两个数相乘,或者先把后两个数想加,积不变
1.4.4.1.1. (×b)×c=a×(b×c)
1.4.5. 乘法分配律
1.4.5.1. 两个数相加(或相减)再乘另一个数,等于这个数分别同两个加数(减数)相乘,再将两个积数相加(相减),得数不变
1.4.5.1.1. (a+b)×c=a×c+b×c
1.4.6. 连减运算
1.4.6.1. 一个数连续减两个数,等于这个数减后两个数的和,得数不变
1.4.6.1.1. a-b-c=a-(b+c)
1.4.6.2. 在三个数的一级运算中,交换后两个数的位置,得数不变
1.4.6.2.1. a-b-c=a-c-b
1.4.7. 连除运算
1.4.7.1. 一个数连续除以两个数,等于这个数除以后两数的积,得数不变
1.4.7.1.1. a÷b÷c=a÷(b×c)
1.4.7.2. 在三个数的二级运算中,交换后两个数的位置,得数不变,
1.4.7.2.1. a÷b÷c=a÷c÷b

一、为什么画混合运算的思维导图
思维导图作为一种有序梳理思路的工具,其作用有很多,其中包括:1、清晰的结构化:通过思维导图的节点和分支,可以清晰地显示混合运算中各个元素之间的关系和层级结构。
2、提升思维的连贯性:通过思维导图的分支和连接,可以帮助你将混合运算中的不同要素进行组织和关联。有助于你更好地理解不同要素之间的逻辑关系,促进思维的连贯性和逻辑性。
3、复习和梳理知识:思维导图可用于有序地梳理知识,通过绘制混合运算的思维导图,你可以整理和总结相关知识点,加深对混合运算概念的理解。
二、混合运算的知识内容梳理
分享混合运算的思维导图前,首先给大家梳理一下混合运算的相关知识内容:1、运算概念

2、运算顺序

3、0的运算

4、运算定律

三、混合运算的思维导图
关于绘制混合运算的思维导图,通常可以使用迅捷思维导图工具进行,这是一款好用的思维导图绘制工具,只需将混合运算的相关知识内容有序地填充至编辑器内即可简单绘制对应的思维导图,同时还附带有“ai助手”和“ai聊天机器人”,可以帮助您轻松整理思路与绘制思维导图。
1、首先进入到迅捷思维导图的编辑页面;
2、接着将需要梳理的内容呈现至编辑器的中心节点内,即:混合运算;
3、随后以层层递进的方式有序将混合运算相关知识内容填充至分支节点;
4、后续还可以通过插入图标、图片、备注或修改主题、样式等方式进一步完善混合运算的思维导图;
5、当混合运算的思维导图绘制完毕后,将图示存储为png、pdf、json等格式即可。

四、《混合运算的思维导图》大纲
1.1. 运算概念1.1.1. 四则运算
1.1.1.1. 加法、减法、乘法和除法统称为四则运算
1.1.2. 四则混合运算
1.1.2.1. 包括有加减乘除及括号的算式运算
1.2. 运算顺序
1.2.1. 无括号
1.2.1.1. 同级运算从左至右依次运算
1.2.1.2. 含两级运算的算式,先乘除,后加减
1.2.2. 有括号
1.2.2.1. 计算顺序
1.2.2.1.1. 小括号-->中括号-->大括号
1.2.2.2. 计算方法
1.2.2.2.1. 先算括号里,再算括号外
1.3. 0的运算
1.3.1. 0不能做除数
1.3.1.1. 如:a÷0(错误表达)
1.3.2. 一个数加上0等于原数
1.3.2.1. a+0=a
1.3.3. 一个数减去0等于原数
1.3.3.1. a-0=a
1.3.4. 一个数减去它本身等于0
1.3.4.1. a-a=0
1.3.5. 一个数乘以0则等于0
1.3.5.1. a×0=0
1.3.6. 0除以任何非0数等于0
1.3.6.1. 0÷a(a≠0)=0
1.4. 运算定律
1.4.1. 加法交换律
1.4.1.1. 两个数的加法运算中,交换加数位置,和不变
1.4.1.1.1. a+b=b+a
1.4.2. 加法结合律
1.4.2.1. 三个数相加,先把前两个数相加,或者先把后两个数相加,和不变
1.4.2.1.1. (a+b)+c=a+(b+c)
1.4.3. 乘法交换律
1.4.3.1. 两个数相乘的乘法运算中,交换两乘数位置,积不变
1.4.3.1.1. a×b=b×a
1.4.4. 乘法结合律
1.4.4.1. 三个数相乘,先把前两个数相乘,或者先把后两个数想加,积不变
1.4.4.1.1. (×b)×c=a×(b×c)
1.4.5. 乘法分配律
1.4.5.1. 两个数相加(或相减)再乘另一个数,等于这个数分别同两个加数(减数)相乘,再将两个积数相加(相减),得数不变
1.4.5.1.1. (a+b)×c=a×c+b×c
1.4.6. 连减运算
1.4.6.1. 一个数连续减两个数,等于这个数减后两个数的和,得数不变
1.4.6.1.1. a-b-c=a-(b+c)
1.4.6.2. 在三个数的一级运算中,交换后两个数的位置,得数不变
1.4.6.2.1. a-b-c=a-c-b
1.4.7. 连除运算
1.4.7.1. 一个数连续除以两个数,等于这个数除以后两数的积,得数不变
1.4.7.1.1. a÷b÷c=a÷(b×c)
1.4.7.2. 在三个数的二级运算中,交换后两个数的位置,得数不变,
1.4.7.2.1. a÷b÷c=a÷c÷b